
| A. | f($\frac{1}{m}$)>-$\frac{1}{m}$ | B. | f($\frac{1}{m}$)>-$\frac{1}{m+1}$ | C. | f($\frac{1}{m+1}$)<$\frac{m}{m+1}$ | D. | f($\frac{1}{m+1}$)<-$\frac{m+2}{m+1}$ |
分析 根据导数的概念得出 $\frac{f(x)-f(0)}{x}$<m<-1,用x=$\frac{1}{m+1}$代入可判断出f( $\frac{1}{m+1}$)>-$\frac{1}{m+1}$,即可判断答案.
解答 解;∵f′(x)=$\underset{lim}{x→0}$$\frac{f(x)-f(0)}{x-0}$,f′(x)<m<-1,
∴$\frac{f(x)-f(0)}{x}$<m<-1,
即 $\frac{f(x)+1}{x}$<m<-1,
当x=$\frac{1}{m+1}$时,f($\frac{1}{m+1}$)+1>$\frac{1}{m+1}$×m=$\frac{m}{m+1}$,
即f($\frac{1}{m+1}$)>$\frac{m}{m+1}$-1=-$\frac{1}{m+1}$,
故f($\frac{1}{m+1}$)>-$\frac{1}{m+1}$,
所以f($\frac{1}{m+1}$)<$\frac{m}{m+1}$,一定出错,
故选:C.
点评 本题考查了导数的概念,不等式的化简运算,属于中档题,理解了变量的代换问题.


科目:高中数学 来源: 题型:解答题
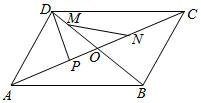 平行四边形ABCD中,对角线AC与BD相交于点O.已知$\overrightarrow{DP}$⊥$\overrightarrow{AC}$,且|$\overrightarrow{DP}$|=2,$\overrightarrow{DM}$=$\frac{1}{3}$$\overrightarrow{DO}$,$\overrightarrow{ON}$=$\frac{1}{3}$$\overrightarrow{OC}$.设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$.
平行四边形ABCD中,对角线AC与BD相交于点O.已知$\overrightarrow{DP}$⊥$\overrightarrow{AC}$,且|$\overrightarrow{DP}$|=2,$\overrightarrow{DM}$=$\frac{1}{3}$$\overrightarrow{DO}$,$\overrightarrow{ON}$=$\frac{1}{3}$$\overrightarrow{OC}$.设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 某几何体的三视图如图所示,若该几何体的体积为5$\sqrt{11}$,则俯视图中线段的长度x的值是( )
某几何体的三视图如图所示,若该几何体的体积为5$\sqrt{11}$,则俯视图中线段的长度x的值是( )| A. | 6 | B. | 4$\sqrt{11}$ | C. | 5 | D. | 2$\sqrt{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,$\frac{3}{2}$) | B. | (1,$\frac{3}{2}$] | C. | [$\frac{1}{2}$,1) | D. | ($\frac{1}{2}$,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | -1 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5+$\sqrt{2}$ | B. | 3+2$\sqrt{2}$ | C. | 8 | D. | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com