Question

2．圆C₁：（y-4）²+x²=2，圆C₂：（y+4）²+x²=2，过C₁点作直线L₁交圆C₁于E、F，过C₂点作直线L₂交圆于M、N，P是平面上一点，且|PC₁|+|PC₂|=10，则$\overrightarrow{PE}$•$\overrightarrow{PF}$+$\overrightarrow{PM}$•$\overrightarrow{PN}$的最小值为46．

Answer 1

分析 由|PC₁|+|PC₂|=10，可知P是椭圆$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{25}$=1上的点，设其点的坐标为（x₀，y₀），再设E、F的坐标为（x₁，y₁），（x₂，y₂），M、N的坐标为（x₃，y₃），（x₄，y₄），根据向量的坐标以及向量的数量积的运算得到$\overrightarrow{PE}$•$\overrightarrow{PF}$+$\overrightarrow{PM}$•$\overrightarrow{PN}$=-$\frac{32}{9}$x₀²+78，再根据-3≤x₀≤3，即可求出最小值．

解答 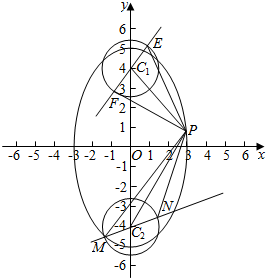解：由|PC₁|+|PC₂|=10，可知P是椭圆$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{25}$=1上的点，设其点的坐标为（x₀，y₀），
再设E、F的坐标为（x₁，y₁），（x₂，y₂），M、N的坐标为（x₃，y₃），（x₄，y₄），
则x₁与x₂，x₃与x₄关于y轴对称，y₁与y₂关于y=4轴对称，y₃与y₄关于y=-4轴对称
∴x₁+x₂=0，x₃+x₄=0，y₁+y₂=8，y₃+y₄=-8，
∴$\overrightarrow{PE}$=（x₁-x₀，y₁-y₀），$\overrightarrow{PF}$=（x₂-x₀，y₂-y₀），$\overrightarrow{PM}$=（x₃-x₀，y₃-y₀），$\overrightarrow{PN}$=（x₄-x₀，y₄-y₀），
∴$\overrightarrow{PE}$•$\overrightarrow{PF}$+$\overrightarrow{PM}$•$\overrightarrow{PN}$=（x₁-x₀，y₁-y₀）•（x₂-x₀，y₂-y₀）+（x₃-x₀，y₃-y₀）•（x₄-x₀，y₄-y₀），
=x₁x₂-x₀（x₁+x₂）+x₀²+y₁y₂-y₀（y₁+y₂）+y₀²+x₃x₄-x₀（x₃+x₄）+x₀²+y₃y₄-y₀（y₃+y₄）+y₀²，
=x₁x₂+x₀²+y₁y₂-8y₀+y₀²+x₃x₄+x₀²+y₃y₄+8y₀+y₀²，
=-x₁²+2x₀²-y₁²+8y₁+2y₀²-x₃²-y₃²-8y₃，
=-[x₁²+（y₁-4）²-16]-[x₃²+（y₃+4）²-16]+2x₀²+2y₀²，
=-（2-16）-（2-16）+2x₀²+2y₀²，
=28+2x₀²+2y₀²，
∵$\frac{{{x}_{0}}^{2}}{9}$+$\frac{{{y}_{0}}^{2}}{25}$=1，
∴$\overrightarrow{PE}$•$\overrightarrow{PF}$+$\overrightarrow{PM}$•$\overrightarrow{PN}$=28+2x₀²+2（25-$\frac{25}{9}$x₀²）=-$\frac{32}{9}$x₀²+78，
∵-3≤x₀≤3
当x₀=3或-3时，有最小值，即为46．

点评 本题考查了圆的方程椭圆的定义以及方程，向量的坐标运算和向量的数量积的运算，培养学生的运算能力，转化能力，属于难题．