
分析 由$\overrightarrow{a}$的坐标求得|$\overrightarrow{a}$|,再由($\overrightarrow{a}$+2$\overrightarrow{b}$)⊥$\overrightarrow{a}$,($\overrightarrow{a}$+$\overrightarrow{b}$)⊥$\overrightarrow{b}$,得$|\overrightarrow{a}{|}^{2}+2\overrightarrow{a}•\overrightarrow{b}=0$,$|\overrightarrow{b}{|}^{2}+\overrightarrow{a}•\overrightarrow{b}=0$,联立即可求得|$\overrightarrow{b}$|.
解答 解:∵$\overrightarrow{a}$=(-$\sqrt{3}$,1),
∴$|\overrightarrow{a}|=2$.
由($\overrightarrow{a}$+2$\overrightarrow{b}$)⊥$\overrightarrow{a}$,($\overrightarrow{a}$+$\overrightarrow{b}$)⊥$\overrightarrow{b}$,
得($\overrightarrow{a}$+2$\overrightarrow{b}$)•$\overrightarrow{a}$=0,($\overrightarrow{a}$+$\overrightarrow{b}$)•$\overrightarrow{b}$=0,
即$|\overrightarrow{a}{|}^{2}+2\overrightarrow{a}•\overrightarrow{b}=0$,①
$|\overrightarrow{b}{|}^{2}+\overrightarrow{a}•\overrightarrow{b}=0$,②
①-②×2得:$|\overrightarrow{a}{|}^{2}=2|\overrightarrow{b}{|}^{2}$,则$|\overrightarrow{b}|$=$\sqrt{\frac{|\overrightarrow{a}{|}^{2}}{2}}=\sqrt{2}$.
故答案为:$\sqrt{2}$.
点评 本题考查平面向量的数量积运算,关键是熟记数量积公式,是中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
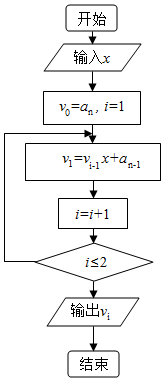 我国古代秦九韶算法可计算多项式anxn+an-1xn-1+…+a1x+a0的值,它所反映的程序框图如图所示,当x=1时,当多项式为x4+4x3+6x2+4x+1的值为( )
我国古代秦九韶算法可计算多项式anxn+an-1xn-1+…+a1x+a0的值,它所反映的程序框图如图所示,当x=1时,当多项式为x4+4x3+6x2+4x+1的值为( )| A. | 5 | B. | 16 | C. | 15 | D. | 11 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | 20 | C. | 26 | D. | 32 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{6}$+$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,$\sqrt{2}$) | B. | (1,$\sqrt{2}$] | C. | ($\sqrt{2}$,+∞) | D. | [$\sqrt{2}$,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com