
【题目】已知椭圆![]() :
:![]() 的一个焦点为
的一个焦点为![]() ,离心率为
,离心率为![]() .
.
(1)求![]() 的标准方程;
的标准方程;
(2)若动点![]() 为
为![]() 外一点,且
外一点,且![]() 到
到![]() 的两条切线相互垂直,求
的两条切线相互垂直,求![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(3)设![]() 的另一个焦点为
的另一个焦点为![]() ,自直线
,自直线![]() :
:![]() 上任意一点
上任意一点![]() 引(2)所求轨迹
引(2)所求轨迹![]() 的一条切线,切点为
的一条切线,切点为![]() ,求证:
,求证:![]() .
.
【答案】(1)![]() (2)
(2)![]() (3)证明见解析
(3)证明见解析
【解析】
(1)根据离心率和焦点坐标可求得![]() 的值,进而得到椭圆的方程;
的值,进而得到椭圆的方程;
(2)设![]() ,切点分别为
,切点分别为![]() ,
,![]() ,对点
,对点![]() 的位置进行讨论,即切线
的位置进行讨论,即切线![]() 的斜率不存在和存在时;当
的斜率不存在和存在时;当![]() 设切线方程为
设切线方程为![]() 代入椭圆的方程得到关于
代入椭圆的方程得到关于![]() 的二次方程,利用直线互相垂直得到
的二次方程,利用直线互相垂直得到![]() 的关系,从而得到点
的关系,从而得到点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(3)设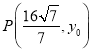 ,将
,将![]() ,
,![]() 都用
都用![]() 进行表示,即可得答案.
进行表示,即可得答案.
(1)设![]() ,
,
由题设,得![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,
,
所以![]() 的标准方程为
的标准方程为![]() .
.
(2)设![]() ,切点分别为
,切点分别为![]() ,
,![]() ,
,
当![]() 时,设切线方程为
时,设切线方程为![]() ,
,
联立方程,得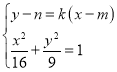 ,
,
消去![]() ,得
,得![]() ,①
,①
关于![]() 的方程①的判别式
的方程①的判别式![]() ,
,
化简,得![]() ,②
,②
关于![]() 的方程②的判别式
的方程②的判别式![]()
![]() ,
,
因为![]() 在椭圆
在椭圆![]() 外,
外,
所以![]() ,即
,即![]() ,所以
,所以![]() ,
,
关于![]() 的方程②有两个实根
的方程②有两个实根![]() ,
,![]() 分别是切线
分别是切线![]() ,
,![]() 的斜率.
的斜率.
因为![]() ,所以
,所以![]() ,即
,即![]() ,化简为
,化简为![]() .
.
当![]() 时,可得
时,可得![]() ,满足
,满足![]() ,
,
所以![]() 的轨迹方程为
的轨迹方程为![]() .
.
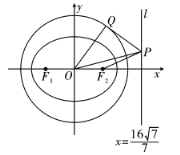
(3)如图,![]() ,设
,设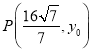 ,
,
![]() ,
,
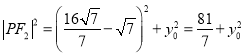 ,
,
所以![]() ,即
,即![]() .
.


 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源: 题型:
【题目】3个红球与3个黑球随机排成一行,从左到右依次在球上标记1,2,3,4,5,6,则红球上的数字之和小于黑球上的数字之和的概率为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】德国著名数学家狄利克雷(Dirichlet,1805~1859)在数学领域成就显著.19世纪,狄利克雷定义了一个“奇怪的函数” 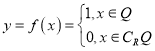 其中R为实数集,Q为有理数集.则关于函数
其中R为实数集,Q为有理数集.则关于函数![]() 有如下四个命题,正确的为( )
有如下四个命题,正确的为( )
A.函数![]() 是偶函数
是偶函数
B.![]() ,
,![]() ,
,![]() 恒成立
恒成立
C.任取一个不为零的有理数T,![]() 对任意的
对任意的![]() 恒成立
恒成立
D.不存在三个点![]() ,
,![]() ,
,![]() ,使得
,使得![]() 为等腰直角三角形
为等腰直角三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设各项均为正数的数列![]() 的前
的前![]() 项和为
项和为![]() ,已知
,已知![]() ,且
,且![]() 对一切
对一切![]() 都成立.
都成立.
(1)当![]() 时.
时.
①求数列![]() 的通项公式;
的通项公式;
②若![]() ,求数列
,求数列![]() 的前
的前![]() 项的和
项的和![]() ;
;
(2)是否存在实数![]() ,使数列
,使数列![]() 是等差数列.如果存在,求出
是等差数列.如果存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】工作人员需进入核电站完成某项具有高辐射危险的任务,每次只派一个人进去,且每个人只派一次,工作时间不超过10分钟,如果前一个人10分钟内不能完成任务则撤出,再派下一个人.现在一共只有甲、乙、丙三个人可派,他们各自能完成任务的概率分别为![]() ,
,![]() ,
,![]() ,假设
,假设![]() ,
,![]() ,
,![]() 互不相等,且假定各人能否完成任务的事件相互独立.
互不相等,且假定各人能否完成任务的事件相互独立.
(1)如果按甲最先,乙次之,丙最后的顺序派人,求任务能被完成的概率.若改变三个人被派出的先后顺序,任务能被完成的概率是否发生变化?
(2)假定![]() ,试分析以怎样的先后顺序派出人员,可使所需派出的人员数目的数学期望达到最小.
,试分析以怎样的先后顺序派出人员,可使所需派出的人员数目的数学期望达到最小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为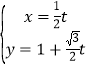 (
(![]() 为参数),在以坐标原点为极点,
为参数),在以坐标原点为极点,![]() 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() (
(![]() 且
且![]() ).
).
(I)求直线![]() 的极坐标方程及曲线
的极坐标方程及曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)已知![]() 是直线
是直线![]() 上的一点,
上的一点,![]() 是曲线
是曲线![]() 上的一点,
上的一点, ![]() ,
,![]() ,若
,若![]() 的最大值为2,求
的最大值为2,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于数列![]() ,若满足
,若满足![]() ,则称数列
,则称数列![]() 为“0-1数列”.定义变换
为“0-1数列”.定义变换![]() ,
,![]() 将“0-1数列”
将“0-1数列”![]() 中原有的每个1都变成0,1,原有的每个0都变成1,0.例如
中原有的每个1都变成0,1,原有的每个0都变成1,0.例如![]() :1,0,1,则
:1,0,1,则![]() 设
设![]() 是“0-1数列”,令
是“0-1数列”,令![]()
![]() 3,….
3,….
(Ⅰ) 若数列![]() :
:![]() 求数列
求数列![]() ;
;
(Ⅱ) 若数列![]() 共有10项,则数列
共有10项,则数列![]() 中连续两项相等的数对至少有多少对?请说明理由;
中连续两项相等的数对至少有多少对?请说明理由;
(Ⅲ)若![]() 为0,1,记数列
为0,1,记数列![]() 中连续两项都是0的数对个数为
中连续两项都是0的数对个数为![]() ,
,![]() .求
.求![]() 关于
关于![]() 的表达式.
的表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com