
| A. | ①③ | B. | ①④ | C. | ②③ | D. | ②④ |
分析 ①根据分段函数的表达式分别求出对应的取值范围进行判断,
②由g(x)=0转化为f(x)=k,解方程即可.
③利用图象进行判断,
④根据函数奇偶性的对称性结合图象进行判断.
解答  解:作出函数f(x)的图象如图:
解:作出函数f(x)的图象如图:
①当x<1时,f(x)=2x-1∈(-1,1),
当x>1时,f(x)=1+log${\;}_{\frac{1}{2}}$x<1,
综上f(x)<1,
即f(x)的值域是(-∞,1);故①错误,
②由g(x)=f(x)-k=0得f(x)=k,
当$k=-\frac{1}{2}$时,若x<1,由f(x)=2x-1=-$\frac{1}{2}$,得2x=$\frac{1}{2}$,即x=-1
当x=1时,f(1)=-$\frac{1}{2}$,
当x>1时,由f(x)=1+log${\;}_{\frac{1}{2}}$x=-$\frac{1}{2}$,得log${\;}_{\frac{1}{2}}$x=-$\frac{3}{2}$,即x=$(\frac{1}{2})^{-\frac{3}{2}}$=${2}^{\frac{3}{2}}=\sqrt{{2}^{3}}$=$2\sqrt{2}$
则g(x)的所有零点之和等于-1+1+$2\sqrt{2}$=$2\sqrt{2}$,故②正确;
③由g(x)=f(x)-k=0得f(x)=k,
由图象知当k≤-1时,g(x)有且仅有一个零点,故③正确;
④若f(x+1)是偶函数则函数f(x+1)关于x=0对称,向右平移1个单位得到f(x),则f(x)关于x=1对称,
当x<1时,f(x)=2x-1∈(-1,1),当x>1时,f(x)=1+log${\;}_{\frac{1}{2}}$x<1,显然关于x=1不对称,故f(x+1)不是偶函数,故④错误,
故正确的是②③,
故选:C
点评 本题主要考查命题的真假判断,涉及分段函数的应用,考查学生分析问题,解决问题的能力,注意使用数形结合以及分类讨论的思想.


科目:高中数学 来源: 题型:选择题
| A. | 10+6i | B. | 8+6i | C. | 8-6i | D. | 10-6i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | C=0,B>0 | B. | A>0,B>0,C=0 | C. | AB<0,C=0 | D. | C=0,AB>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=AD=2,四边形ABCD满足AB⊥AD,BC∥AD且BC=4,点M为PC的中点,点E为BC边上的点,且$\frac{BE}{EC}$=λ.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=AD=2,四边形ABCD满足AB⊥AD,BC∥AD且BC=4,点M为PC的中点,点E为BC边上的点,且$\frac{BE}{EC}$=λ.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
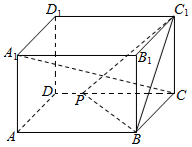 如图,长方体ABCD-A1B1C1D1中,AB=2,BC=CC1=1,点P是CD上的一点,PC=λPD.
如图,长方体ABCD-A1B1C1D1中,AB=2,BC=CC1=1,点P是CD上的一点,PC=λPD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 某几何体的三视图如图所示(单位:cm),则该几何体的体积是( )cm3.
某几何体的三视图如图所示(单位:cm),则该几何体的体积是( )cm3.| A. | 1+2π | B. | 1+$\frac{4π}{3}$ | C. | 1+$\frac{π}{2}$ | D. | 1+$\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 若某空间几何体的三视图如图所示,根据图中数据,可得该几何体的外接球的体积是( )
若某空间几何体的三视图如图所示,根据图中数据,可得该几何体的外接球的体积是( )| A. | $\frac{{\sqrt{2}}}{3}$π | B. | $\frac{4}{3}$π | C. | $\sqrt{6}$π | D. | 8$\sqrt{6}$π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com