
| A. | (-∞,1-e) | B. | (1-e,1] | C. | [1,e-1) | D. | (e-1,+∞) |
分析 根据题意,不等式x+$\frac{1}{{e}^{x}}$>ax恒成立化为$\frac{1}{{e}^{x}}$>(a-1)x恒成立;
设g(x)=$\frac{1}{{e}^{x}}$,h(x)=(a-1)x,x∈R;
在同一坐标系内画出两个函数的图象,满足不等式恒成立的是h(x)的图象在g(x)图象下方,
求出过原点的g(x)的切线方程,得出切线斜率k,从而求出a的取值范围.
解答 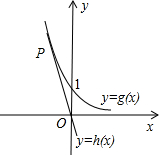 解:函数$f(x)=x+\frac{1}{e^x}$,对任意x∈R,f(x)>ax恒成立,
解:函数$f(x)=x+\frac{1}{e^x}$,对任意x∈R,f(x)>ax恒成立,
∴x+$\frac{1}{{e}^{x}}$>ax恒成立,
即$\frac{1}{{e}^{x}}$>(a-1)x恒成立;
设g(x)=$\frac{1}{{e}^{x}}$,h(x)=(a-1)x,x∈R;
在同一坐标系内画出两个函数的图象,如图所示;
则满足不等式恒成立的是h(x)的图象在g(x)图象下方,
求g(x)的导数g′(x)=-e-x,
且过g(x)图象上点(x0,y0)的切线方程为
y-y0=-${e}^{{-x}_{0}}$(x-x0),
且该切线方程过原点(0,0),
则y0=-${e}^{{-x}_{0}}$•x0,
即${e}^{{-x}_{0}}$=-${e}^{{-x}_{0}}$•x0,
解得x0=-1;
∴切线斜率为k=-${e}^{{-x}_{0}}$=-e,
∴应满足0≥a-1>-e,
∴1-e<a≤1,
∴实数a的取值范围是(1-e,1].
故选:B.
点评 本题考查了函数的性质与应用问题,也考查了利用导数求函数的切线问题,是综合性题目.


科目:高中数学 来源: 题型:选择题
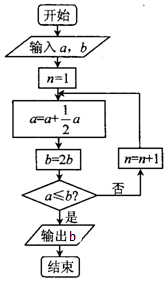 宋元时期数学名著《算学启蒙》中关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等,如图是源于其思想的一个程序框图,若输入的a,b分别为5,2,则输出的b=( )
宋元时期数学名著《算学启蒙》中关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等,如图是源于其思想的一个程序框图,若输入的a,b分别为5,2,则输出的b=( )| A. | 8 | B. | 16 | C. | 32 | D. | 64 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,2] | B. | [1,2) | C. | [-2,∞) | D. | (-2,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | z=-3+i | B. | $\overline z=3-i$ | C. | z=1-3i | D. | $\overline z=-1+3i$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
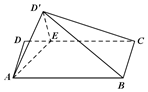 如图,矩形ABCD中,AB=4,AD=2,E在DC边上,且DE=1,将△ADE沿AE折到△AD'E的位置,使得平面AD'E⊥平面ABCE.
如图,矩形ABCD中,AB=4,AD=2,E在DC边上,且DE=1,将△ADE沿AE折到△AD'E的位置,使得平面AD'E⊥平面ABCE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{3}$,1) | B. | (-∞,$\frac{1}{3}$)∪(1,+∞) | C. | (-$\frac{1}{3}$,1) | D. | D、(-∞,$-\frac{1}{3}$)∪($\frac{1}{3}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,点A(2,0),直线l垂直y轴,垂足为点B,线段AB的垂直平分线与l相交于点C,
如图,点A(2,0),直线l垂直y轴,垂足为点B,线段AB的垂直平分线与l相交于点C,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 喜欢甜品 | 不喜欢甜品 | 合计 | |
| 南方学生 | 60 | 20 | 80 |
| 北方学生 | 10 | 10 | 20 |
| 合计 | 70 | 30 | 100 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com