
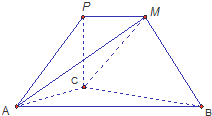
 如图,PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2,又AC=1,∠ACB=120°,AB⊥PC,直线AM与直线PC所成的角为60°
如图,PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2,又AC=1,∠ACB=120°,AB⊥PC,直线AM与直线PC所成的角为60°分析 (1)通过证明PC⊥平面ABC得出平面PCBM⊥平面ABC;
(1)取BC的中点为O,连接MO,则可证OM⊥平面ABC,∠AMO=60°,从而求得OM的长,代入棱锥的体积公式VB-CMA=VM-ABC=$\frac{1}{3}{S}_{△ABC}•OM$计算即可.
解答  证明:(1)∵PC⊥AB,PC⊥BC,AB∩BC=B,
证明:(1)∵PC⊥AB,PC⊥BC,AB∩BC=B,
∴PC∩平面ABC,又PC?平面PCBM,
∴平面PCBM⊥平面ABC.
(2)取BC的中点为O,连接MO.
∵PM∥BC,又PM=$\frac{1}{2}$BC,
∴四边形PMOC为平行四边形,
∴PC∥MO,
∵PC⊥平面ABC,
∴MO⊥平面ABC,∠AMO为AM与PC所成的角.即∠AMO=60°,
∵AC=CO=1,∠ACO=120°,
∴AO=$\sqrt{3}$,∴OM=1,
∴VB-CMA=VM-ABC=$\frac{1}{3}{S}_{△ABC}•OM$=$\frac{1}{3}×\frac{1}{2}×2×1×\frac{\sqrt{3}}{2}×1$=$\frac{\sqrt{3}}{6}$.
点评 本题考查了面面垂直的判定定理,棱锥的体积计算,属于中档题.


 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若x>2015,则x>0”的逆命题 | |
| B. | 命题“若xy=0,则x=0或y=0”的否命题 | |
| C. | 命题“若x2+x-2=0,则x=1” | |
| D. | 命题“若x2≥1,则x≥1”的逆否命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=sinx | B. | f(x)=cosx | C. | f(x)=sinxcosx | D. | f(x)=cos2x-sin2x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{8}$ | B. | $-\frac{3}{4}$ | C. | $\frac{9}{8}$ | D. | $\frac{7}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 画出函数y=|x|的图象,并根据图象写出函数的单调区间,以及在各单调区间上,函数是增函数还是减函数.(提示:由绝对值的定义将函数化为分段函数,再画图,不必列表)
画出函数y=|x|的图象,并根据图象写出函数的单调区间,以及在各单调区间上,函数是增函数还是减函数.(提示:由绝对值的定义将函数化为分段函数,再画图,不必列表)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com