
分析 若f(a-2sinx)≤f(cos2x)对一切实数x∈R恒成立,则a≥cos2x+2sinx=1-sin2x+2sinx对一切实数x∈R恒成立,求出1-sin2x+2sinx的最大值,可得答案.
解答 解:∵函数f(x)是定义在R上的单调减函数,
若f(a-2sinx)≤f(cos2x)对一切实数x∈R恒成立,
则a-2sinx≥cos2x对一切实数x∈R恒成立,
即a≥cos2x+2sinx=1-sin2x+2sinx对一切实数x∈R恒成立,
令t=sinx,y=-t2+2t+1,t∈[-1,1],
故t=1时,y取最大值2,
故${\;}_{\;}^{\;}a≥2{\;}_{\;}^{\;}$;
故答案为:${\;}_{\;}^{\;}a≥2{\;}_{\;}^{\;}$
点评 本题考查的知识点是函数恒成立,换元法,函数的最值,函数的单调性,难度中档.


 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
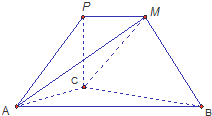 如图,PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2,又AC=1,∠ACB=120°,AB⊥PC,直线AM与直线PC所成的角为60°
如图,PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2,又AC=1,∠ACB=120°,AB⊥PC,直线AM与直线PC所成的角为60°查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com