
| A. | f(x)=sinx | B. | f(x)=cosx | C. | f(x)=sinxcosx | D. | f(x)=cos2x-sin2x |
分析 根据题意,要求函数满足条件,则该函数必须是奇函数且周期为π,据此由三角函数的性质依次分析选项四个函数的奇偶性与周期性即可得答案.
解答 解:根据题意,要求函数满足条件f(-x)+f(x)=0和$f(\frac{π}{2}-x)=f(x)$则该函数必须是奇函数且周期为π,
据此依次分析选项可得:
对于A、f(x)=sinx是奇函数且周期为2π,不符合题意;
对于B、f(x)=cosx是偶函数且周期为2π,不符合题意;
对于C、f(x)=sinxcosx=$\frac{1}{2}$sin2x是奇函数且周期为π,符合题意;
对于D、f(x)=ccos2x-sin2x=cos2x是偶函数且周期为π,不符合题意;
故选:C.
点评 本题考查三角函数的性质,关键是分析出函数的周期与奇偶性.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
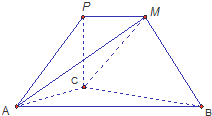 如图,PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2,又AC=1,∠ACB=120°,AB⊥PC,直线AM与直线PC所成的角为60°
如图,PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2,又AC=1,∠ACB=120°,AB⊥PC,直线AM与直线PC所成的角为60°查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | [-2,-1] | B. | [-2,1) | C. | [-1,1) | D. | [-1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
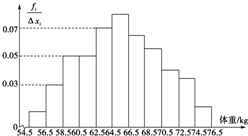 为了了解某地区高二学生的身体发育情况,抽查了该地区100名年龄为16.5岁~18岁的男生体重(kg),得到频率分布直方图如图所示.根据此图可得这100名学生中体重在[56.5,64.5)内的学生人数是( )
为了了解某地区高二学生的身体发育情况,抽查了该地区100名年龄为16.5岁~18岁的男生体重(kg),得到频率分布直方图如图所示.根据此图可得这100名学生中体重在[56.5,64.5)内的学生人数是( )| A. | 2 | B. | 30 | C. | 40 | D. | 50 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com