
设函数f(x)=cln x+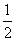 x2+bx(b,c∈R,c≠0),且x=1为f(x)的极值点.
x2+bx(b,c∈R,c≠0),且x=1为f(x)的极值点.
(1)若x=1为f(x)的极大值点,求f(x)的单调区间(用c表示);
(2)若f(x)=0恰有两解,求实数c的取值范围.
解:f′(x)=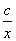 +x+b=
+x+b=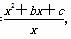 ,又f′(1)=0,
,又f′(1)=0,
则b+c+1=0,
所以f′(x)=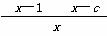 且c≠1,
且c≠1,
(1)因为x=1为f(x)的极大值点,所以c>1.
令f′(x)>0,得0<x<1或x>c;令f′(x)<0,得1<x<c.
所以f(x)的递增区间为(0,1),(c,+∞);递减区间为(1,c).
(2)①若c<0,则f(x)在(0,1)上递减,在(1,+∞)上递增.
若f(x)=0恰有两解,则f(1)<0,即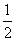 +b<0,所以-
+b<0,所以-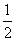 <c<0.
<c<0.
②若0<c<1,则f(x)极大值=f(c)=cln c+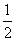 c2+bc,f(x)极小值=f(1)=
c2+bc,f(x)极小值=f(1)=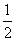 +b.因为b=-1-c,
+b.因为b=-1-c,
则f(x)极大值=cln c+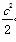 +c(-1-c)=cln c-c-
+c(-1-c)=cln c-c-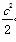 <0,
<0,
f(x)极小值=-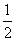 -c,从而f(x)=0只有一解;
-c,从而f(x)=0只有一解;
③若c>1,则f(x)极大值=-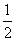 -c<0,
-c<0,
从而f(x)极小值=cln c+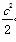 +c(-1-c)
+c(-1-c)
=cln c-c-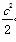 <0,
<0,
则f(x)=0只有一解.
综上,使f(x)=0恰有两解的c的取值范围为-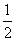 <c<0.
<c<0.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
已知集合A={x|x2-2x-3≤0},B={x|m-2≤x≤m+2,m∈R}.
(1)若A∪B=A,求实数m的取值;
(2)若A∩B={x|0≤x≤3},求实数m的值;
(3)若A⊆∁RB,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)在实数集R上具有下列性质:①直线x=1是函数f(x)的一条对称轴;②f(x+2)=-f(x);③当1≤x1<x2≤3时,(f(x2)-f(x1))·(x2-x1)<0,则f(2 011)、f(2 012)、f(2 013)从大到小的顺序为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
若二次函数f(x)=ax2+bx+c(a≠0)满足f(x+1)-f(x)=2x,且f(0)=1.
(1)求f(x)的解析式;
(2)若在区间[-1,1]上,不等式f(x)>2x+m恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
若商品的年利润y(万元)与年产量x(百万件)的函数关系式y=-x3+27x+123(x>0),则获得最大利润时的年产量为( )
A.1百万件 B.2百万件
C.3百万件 D.4百万件
查看答案和解析>>
科目:高中数学 来源: 题型:
对于R上可导的任意函数f(x),若满足(x-1)f′(x)≥0,则必有( )
A.f(0)+f(2)<2f(1) B.f(0)+f(2)≤2f(1)
C.f(0)+f(2)≥2f(1) D.f(0)+f(2)>2f(1)
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=x-aln x(a∈R).
(1)当a=2时,求曲线y=f(x)在点A(1, f(1))处的切线方程;
(2)求函数f(x)的极值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com