
分析 (1)${S_n}={n^2}+kn$,n≥2时,an=Sn-Sn-1.n=6时,a6=13,解得k.进而得出.
(2)${b_n}=\frac{2}{{n({a_n}+1)}}$=$\frac{2}{n(2n+2)}$=$\frac{1}{n(n+1)}$=$\frac{1}{n}-\frac{1}{n+1}$,利用“裂项求和”方法即可得出.
解答 解:(1)∵${S_n}={n^2}+kn$,n≥2时,an=Sn-Sn-1=n2+kn-[(n-1)2+k(n-1)]=2n-1+k.
∴n=6时,a6=11+k=13,解得k=2.
∴n≥2时,an=2n-1+2=2n+1.
当n=1时,a1=S1=1+2=3,上式也成立.
∴an=2n+1.
(2)${b_n}=\frac{2}{{n({a_n}+1)}}$=$\frac{2}{n(2n+2)}$=$\frac{1}{n(n+1)}$=$\frac{1}{n}-\frac{1}{n+1}$,
数列{bn}的前n项和Tn=$(1-\frac{1}{2})+(\frac{1}{2}-\frac{1}{3})$+…+$(\frac{1}{n}-\frac{1}{n+1})$=1-$\frac{1}{n+1}$=$\frac{n}{n+1}$.
点评 本题考查了递推关系、数列的通项公式、“裂项求和”方法,考查了推理能力与计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | (0,1) | C. | [1,+∞) | D. | (-∞,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
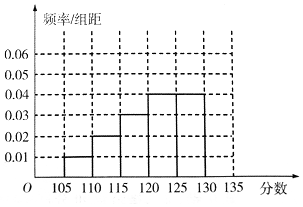 某次数学测试之后,数学组的老师对全校数学总成绩分布在[105,135)的n名同学的19题成绩进行了分析,数据整理如下:
某次数学测试之后,数学组的老师对全校数学总成绩分布在[105,135)的n名同学的19题成绩进行了分析,数据整理如下:| 组数 | 分组 | 19题满分人数 | 19题满分人数占本组人数比例 |
| 第一组 | [105,110] | 15 | 0.3 |
| 第二组 | [110,115) | 30 | 0.3 |
| 第三组 | [115,120) | x | 0.4 |
| 第四组 | [120,125) | 100 | 0.5 |
| 第五组 | [125,130) | 120 | 0.6 |
| 第六组 | [130,135) | 195 | y |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在多面体ABCDPE中,四边形ABCD和CDPE都是直角梯形,AB∥DC,PE∥DC,AD⊥DC,PD⊥平面ABCD,AB=PD=DA=2PE,CD=3PE,F是CE的中点.
如图,在多面体ABCDPE中,四边形ABCD和CDPE都是直角梯形,AB∥DC,PE∥DC,AD⊥DC,PD⊥平面ABCD,AB=PD=DA=2PE,CD=3PE,F是CE的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 为创建全国文明城市,某区向各事业行政单位征集“文明过马路”义务督导员.从符合条件的600名志愿者中随机抽取100名,按年龄作分组如下:[20,25),[25,30),[30,35),[35,40),[40,45],并得到如下频率分布直方图.
为创建全国文明城市,某区向各事业行政单位征集“文明过马路”义务督导员.从符合条件的600名志愿者中随机抽取100名,按年龄作分组如下:[20,25),[25,30),[30,35),[35,40),[40,45],并得到如下频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
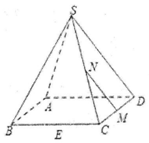 如图,在正四棱锥S-ABCD中,E.M.N分别是BC.CD.SC的中点,动点P的线段MN上运动时,下列四个结论:
如图,在正四棱锥S-ABCD中,E.M.N分别是BC.CD.SC的中点,动点P的线段MN上运动时,下列四个结论:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com