Question

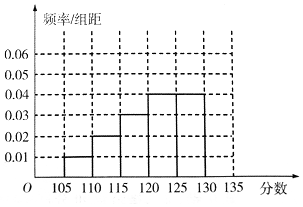
17．某次数学测试之后，数学组的老师对全校数学总成绩分布在[105，135）的n名同学的19题成绩进行了分析，数据整理如下：

组数	分组	19题满分人数	19题满分人数占本组人数比例
第一组	[105，110]	15	0.3
第二组	[110，115）	30	0.3
第三组	[115，120）	x	0.4
第四组	[120，125）	100	0.5
第五组	[125，130）	120	0.6
第六组	[130，135）	195	y

（Ⅰ）补全所给的频率分布直方图，并求n，x，y的值；
（Ⅱ）现从[110，115）、[115，120）两个分数段的19题满分的试卷中，按分层抽样的方法抽取9份进行展出，并从9份试卷中选出两份作为优秀试卷，优秀试卷在[115，120）中的分数记为ξ，求随机变量ξ的分布列及期望．

Answer 1

分析 （I）利用频率分布直方图的性质即可得出．
（II）现从[110，115）、[115，120）两个分数段的19题满分的试卷中，按分层抽样的方法抽取9份进行展出，则分别抽取3，6份．从9份试卷中选出两份作为优秀试卷，优秀试卷在[115，120）中的分数记为ξ，取值为：0，1，2．利用P（ξ=k）=$\frac{{∁}_{3}^{2-k}{∁}_{6}^{k}}{{∁}_{9}^{2}}$即可得出．

解答 解：（I）由第一组[105，110）可得：$\frac{15}{0.01×5n}$=0.3，解得：n=1000．
∴$\frac{x}{0.03×5×1000}$=0.4，解得：x=60．
在区间[1305，135）的频率为z，则（0.01+0.02+0.03+0.04×2+z）×5=1，解得z=0.06．
∴$\frac{195}{0.06×5×1000}$=y，解得y=0.65．
（II）现从[110，115）、[115，120）两个分数段的19题满分的试卷中，按分层抽样的方法抽取9份进行展出，
则分别抽取3，6份．
从9份试卷中选出两份作为优秀试卷，优秀试卷在[115，120）中的分数记为ξ，取值为：0，1，2．
则P（ξ=k）=$\frac{{∁}_{3}^{2-k}{∁}_{6}^{k}}{{∁}_{9}^{2}}$，可得P（ξ=0）=$\frac{3}{36}$，P（ξ=1）=$\frac{18}{36}$，P（ξ=2）=$\frac{{∁}_{6}^{2}}{{∁}_{9}^{2}}$=$\frac{15}{36}$．
ξ的分布列为：

ξ	0	1	2
P	$\frac{3}{36}$	$\frac{18}{36}$	$\frac{15}{36}$

E（ξ）=0+1×$\frac{18}{36}$+2×$\frac{15}{36}$=$\frac{4}{3}$．

点评 本题考查频率分布直方图的性质、分层抽样的方法、超几何分布列及其数学期望的求法，考查推理能力与计算能力，属于中档题．