
分析 由对任意单位向量$\overrightarrow{e}$,均有|$\overrightarrow{a}$•$\overrightarrow{e}$|+|$\overrightarrow{b}$•$\overrightarrow{e}$|≤$\sqrt{6}$,可得|$\overrightarrow{a}$•$\overrightarrow{e}$+$\overrightarrow{b}$•$\overrightarrow{e}$|≤$\sqrt{6}$,即|$\overrightarrow{a}$+$\overrightarrow{b}$|≤$\sqrt{6}$,|$\overrightarrow{a}$-$\overrightarrow{b}$|≤$\sqrt{6}$,⇒|$\overrightarrow{a}$+$\overrightarrow{b}$|2≤6,|$\overrightarrow{a}$-$\overrightarrow{b}$|2≤6,求得$\overrightarrow{a}$$•\overrightarrow{b}$取最小值,再求向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角.
解答 解:∵|$\overrightarrow{a}$•$\overrightarrow{e}$+$\overrightarrow{b}$•$\overrightarrow{e}$|≤|$\overrightarrow{a}$•$\overrightarrow{e}$|+|$\overrightarrow{b}$•$\overrightarrow{e}$|≤$\sqrt{6}$,
且对任意单位向量$\overrightarrow{e}$,均有|$\overrightarrow{a}$•$\overrightarrow{e}$|+|$\overrightarrow{b}$•$\overrightarrow{e}$|≤$\sqrt{6}$,则|$\overrightarrow{a}$•$\overrightarrow{e}$+$\overrightarrow{b}$•$\overrightarrow{e}$|≤$\sqrt{6}$,
⇒|$\overrightarrow{a}$+$\overrightarrow{b}$|≤$\sqrt{6}$,|$\overrightarrow{a}$-$\overrightarrow{b}$|≤$\sqrt{6}$,⇒|$\overrightarrow{a}$+$\overrightarrow{b}$|2≤6,|$\overrightarrow{a}$-$\overrightarrow{b}$|2≤6,⇒$-\frac{1}{2}≤\overrightarrow{a}•\overrightarrow{b}≤\frac{1}{2}$.
$\overrightarrow{a}$$•\overrightarrow{b}$取最小值为-$\frac{1}{2}$,向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为θ,cos$θ=-\frac{1}{4}$,
向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为arccos(-$\frac{1}{4}$),
故答案为:arccos(-$\frac{1}{4}$)
点评 本题考查了向量三角不等式的应用,属于难题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 充分且必要条件 | B. | 既不充分也不必要条件 | ||
| C. | 必要不充分条件 | D. | 充分不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
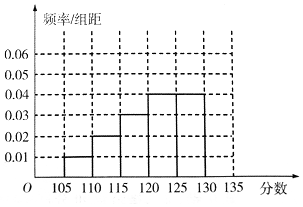 某次数学测试之后,数学组的老师对全校数学总成绩分布在[105,135)的n名同学的19题成绩进行了分析,数据整理如下:
某次数学测试之后,数学组的老师对全校数学总成绩分布在[105,135)的n名同学的19题成绩进行了分析,数据整理如下:| 组数 | 分组 | 19题满分人数 | 19题满分人数占本组人数比例 |
| 第一组 | [105,110] | 15 | 0.3 |
| 第二组 | [110,115) | 30 | 0.3 |
| 第三组 | [115,120) | x | 0.4 |
| 第四组 | [120,125) | 100 | 0.5 |
| 第五组 | [125,130) | 120 | 0.6 |
| 第六组 | [130,135) | 195 | y |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
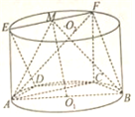 在如图所示的圆柱O1O2中,等腰梯形ABCD内接于下底面圆O1,AB∥CD,且AB为圆O1的直径,EA和FC都是圆柱O1O2的母线,M为线段EF的中点.
在如图所示的圆柱O1O2中,等腰梯形ABCD内接于下底面圆O1,AB∥CD,且AB为圆O1的直径,EA和FC都是圆柱O1O2的母线,M为线段EF的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在多面体ABCDPE中,四边形ABCD和CDPE都是直角梯形,AB∥DC,PE∥DC,AD⊥DC,PD⊥平面ABCD,AB=PD=DA=2PE,CD=3PE,F是CE的中点.
如图,在多面体ABCDPE中,四边形ABCD和CDPE都是直角梯形,AB∥DC,PE∥DC,AD⊥DC,PD⊥平面ABCD,AB=PD=DA=2PE,CD=3PE,F是CE的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 为创建全国文明城市,某区向各事业行政单位征集“文明过马路”义务督导员.从符合条件的600名志愿者中随机抽取100名,按年龄作分组如下:[20,25),[25,30),[30,35),[35,40),[40,45],并得到如下频率分布直方图.
为创建全国文明城市,某区向各事业行政单位征集“文明过马路”义务督导员.从符合条件的600名志愿者中随机抽取100名,按年龄作分组如下:[20,25),[25,30),[30,35),[35,40),[40,45],并得到如下频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com