
分析 (1)根据对数运算性质得$\frac{1+x}{1-x}$=2,从而解出x的值;
(2)令g(x)=$\frac{ax-1}{a-x}$,判断g(x)的单调性得出g(x)的值域,根据对数的运算性质化简即可证明f($\frac{ax-1}{a-x}$)-f(x)=-f($\frac{1}{a}$);
(3)利用(2)中的结论得出f(xn+1)与f(xn)的关系,判断f(xn)的周期,分别用f(x1)表示出f(x2),f(x3),f(x4),根据f(x)的单调性得出$\left\{\begin{array}{l}{f({x}_{3})≥f({x}_{1})}\\{f({x}_{3})≥f({x}_{2})}\\{f({x}_{3})≥f({x}_{4})}\end{array}\right.$,从而求出f(x1)的范围,继而解出x1的范围.
解答 解:(1)∵f(x)=log2$\frac{1+x}{1-x}$=1,
∴$\frac{1+x}{1-x}$=2,解得$x=\frac{1}{3}$;
(2)令g(x)=$\frac{ax-1}{a-x}$,则g′(x)=$\frac{a(a-x)+(ax-1)}{(a-x)^{2}}$=$\frac{{a}^{2}-1}{(a-x)^{2}}$.
∵a∈(1,+∞),∴g′(x)>0,
∴g(x)在(-1,1)上是增函数,
又g(-1)=$\frac{-a-1}{a+1}=-1$,g(1)=$\frac{a-1}{a-1}$=1,
∴-1<g(x)<1,即$\frac{ax-1}{a-x}$∈(-1,1).
∵f(x)-f($\frac{1}{a}$)=log2$\frac{1+x}{1-x}$-log2$\frac{1+\frac{1}{a}}{1-\frac{1}{a}}$=log2$\frac{1+x}{1-x}$-log2$\frac{a+1}{a-1}$
=log2($\frac{1+x}{1-x}•\frac{a-1}{a+1}$)=log2$\frac{ax+a-x-1}{a-x-ax+1}$,
f($\frac{ax-1}{a-x}$)=log2$\frac{1+\frac{ax-1}{a-x}}{1-\frac{ax-1}{a-x}}$=log2$\frac{a-x+ax-1}{a-x-ax+1}$.
∴f($\frac{ax-1}{a-x}$)=f(x)-f($\frac{1}{a}$),
∴f($\frac{ax-1}{a-x}$)-f(x)=-f($\frac{1}{a}$).
(3)∵f(x)的定义域为(-1,1),
f(-x)=log2$\frac{1-x}{1+x}$=-log2$\frac{1+x}{1-x}$=-f(x),
∴f(x)是奇函数.
∵xn+1=(-1)n+1$\frac{{3{x_n}-1}}{{3-{x_n}}}$,
∴xn+1=$\left\{\begin{array}{l}{\frac{3{x}_{n}-1}{3-{x}_{n}},n为奇数}\\{-\frac{3{x}_{n}-1}{3-{x}_{n}},n为偶数}\end{array}\right.$.
①当n为奇数时,f(xn+1)=f($\frac{3{x}_{n}-1}{3-{x}_{n}}$)=f(xn)-f($\frac{1}{3}$)=f(xn)-1,
∴f(xn+1)=f(xn)-1;
②当n为偶数时,f(xn+1)=f(-$\frac{3{x}_{n}-1}{3-{x}_{n}}$)=-f($\frac{3{x}_{n}-1}{3-{x}_{n}}$)=1-f(xn),
∴f(xn+1)=1-f(xn).
∴f(x2)=f(x1)-1,f(x3)=1-f(x2)=2-f(x1),f(x4)=f(x3)-1=1-f(x1),
f(x5)=1-f(x4)=f(x1),f(x6)=f(x5)-1=f(x1)-1,…
∴f(xn)=f(xn+4),n∈N+.
设h(x)=$\frac{1+x}{1-x}$,则h′(x)=$\frac{1-x+1+x}{(1-x)^{2}}$=$\frac{2}{(1-x)^{2}}$>0,
∴h(x)在(-1,1)上是增函数,
∴f(x)=log2$\frac{1+x}{1-x}$=log2h(x)在(-1,1)上是增函数.
∵x3≥xn对任意n∈N*成立,
∴f(x3)≥f(xn)恒成立,
∴$\left\{\begin{array}{l}{f({x}_{3})≥f({x}_{1})}\\{f({x}_{3})≥f({x}_{2})}\\{f({x}_{3})≥f({x}_{4})}\end{array}\right.$,即$\left\{\begin{array}{l}{2-f({x}_{1})≥f({x}_{1})}\\{2-f({x}_{1})≥f({x}_{1})-1}\\{2-f({x}_{1})≥1-f({x}_{1})}\end{array}\right.$,
解得:f(x1)≤1,即log2$\frac{1+{x}_{1}}{1-{x}_{1}}$≤1,
∴0<$\frac{1+{x}_{1}}{1-{x}_{1}}$≤2,
解得:-1<x1≤$\frac{1}{3}$.
点评 本题考查了对数的运算性质,复合函数的单调性,不等式的解法,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | 13 | C. | 14 | D. | 15 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,棱锥P-ABCD的底面ABCD是矩形,PA⊥面ABCD,PA=AD=4,BD=4$\sqrt{2}$,E为PD的中点.
如图,棱锥P-ABCD的底面ABCD是矩形,PA⊥面ABCD,PA=AD=4,BD=4$\sqrt{2}$,E为PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
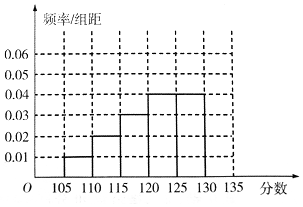 某次数学测试之后,数学组的老师对全校数学总成绩分布在[105,135)的n名同学的19题成绩进行了分析,数据整理如下:
某次数学测试之后,数学组的老师对全校数学总成绩分布在[105,135)的n名同学的19题成绩进行了分析,数据整理如下:| 组数 | 分组 | 19题满分人数 | 19题满分人数占本组人数比例 |
| 第一组 | [105,110] | 15 | 0.3 |
| 第二组 | [110,115) | 30 | 0.3 |
| 第三组 | [115,120) | x | 0.4 |
| 第四组 | [120,125) | 100 | 0.5 |
| 第五组 | [125,130) | 120 | 0.6 |
| 第六组 | [130,135) | 195 | y |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
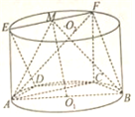 在如图所示的圆柱O1O2中,等腰梯形ABCD内接于下底面圆O1,AB∥CD,且AB为圆O1的直径,EA和FC都是圆柱O1O2的母线,M为线段EF的中点.
在如图所示的圆柱O1O2中,等腰梯形ABCD内接于下底面圆O1,AB∥CD,且AB为圆O1的直径,EA和FC都是圆柱O1O2的母线,M为线段EF的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在多面体ABCDPE中,四边形ABCD和CDPE都是直角梯形,AB∥DC,PE∥DC,AD⊥DC,PD⊥平面ABCD,AB=PD=DA=2PE,CD=3PE,F是CE的中点.
如图,在多面体ABCDPE中,四边形ABCD和CDPE都是直角梯形,AB∥DC,PE∥DC,AD⊥DC,PD⊥平面ABCD,AB=PD=DA=2PE,CD=3PE,F是CE的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com