
| A. | x+4y+2=0 | B. | x+4y-2=0 | C. | x+y+2=0 | D. | x+y-2=0 |
分析 设切点为(x0,y0),则y0=$\frac{1}{{x}_{0}}$,由于直线l经过(2,0),推出切线的斜率,再根据导数的几何意义求出曲线在点x0处的切线斜率,便可建立关于x0的方程.求出x0,然后求解切线方程.
解答 解:设直线l:y=k(x-1).∵曲线$y=\frac{1}{x}$,∴y′=-$\frac{1}{{x}^{2}}$,∴$y′{|}_{x={x}_{0}}$=-$\frac{1}{{{x}_{0}}^{2}}$
设曲线的切点(x0,y0)(x0≠0),则k=$\frac{{y}_{0}-0}{{x}_{0}-2}$,
∴-$\frac{1}{{{x}_{0}}^{2}}$=$\frac{1}{{{x}_{0}}^{2}-2{x}_{0}}$,∵x0≠0,∴x0=1,∴k=-1,
故直线l的方程为:x+y-2=0.
故选:D.
点评 此题考查学生会利用导数求曲线上过某点切线方程的斜率,会根据一点坐标和斜率写出直线的方程,是一道综合题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | (0,1) | C. | [1,+∞) | D. | (-∞,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
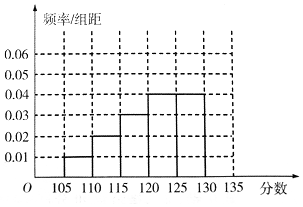 某次数学测试之后,数学组的老师对全校数学总成绩分布在[105,135)的n名同学的19题成绩进行了分析,数据整理如下:
某次数学测试之后,数学组的老师对全校数学总成绩分布在[105,135)的n名同学的19题成绩进行了分析,数据整理如下:| 组数 | 分组 | 19题满分人数 | 19题满分人数占本组人数比例 |
| 第一组 | [105,110] | 15 | 0.3 |
| 第二组 | [110,115) | 30 | 0.3 |
| 第三组 | [115,120) | x | 0.4 |
| 第四组 | [120,125) | 100 | 0.5 |
| 第五组 | [125,130) | 120 | 0.6 |
| 第六组 | [130,135) | 195 | y |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com