
分析 先写出$f(x)=(\frac{1}{2})^{2x}-3•(\frac{1}{2})^{x}+2$,从而可设$(\frac{1}{2})^{x}=t$,根据x的范围即可求出t的范围,进而得到二次函数y=t2-3t+2,这样配方求该函数的值域即可得出f(x)的值域.
解答 解:$f(x)=(\frac{1}{2})^{2x}-3•(\frac{1}{2})^{x}+2$,-2≤x≤2;
设$(\frac{1}{2})^{x}=t$,则$\frac{1}{4}≤t≤4$;
∴$y={t}^{2}-3t+2=(t-\frac{3}{2})^{2}-\frac{1}{4}$;
∴$t=\frac{3}{2}$时,${y}_{min}=-\frac{1}{4}$,t=4时,ymax=6;
∴f(x)的值域为$[-\frac{1}{4},6]$.
故答案为:$[-\frac{1}{4},6]$.
点评 考查指数式的运算,换元法求函数的值域,以及配方求二次函数值域的方法.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{1}{e}$) | B. | (-∞,$\frac{1}{\sqrt{e}}$) | C. | (-∞,$\sqrt{e}$) | D. | (-∞,e) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
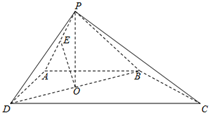 如图,四棱锥P-ABCD的底面是直角梯形,AB∥CD,AB⊥AD,△PAB和△PAD是两个边长为2的正三角形,DC=4,O为BD的中点,E为PA的一动点.
如图,四棱锥P-ABCD的底面是直角梯形,AB∥CD,AB⊥AD,△PAB和△PAD是两个边长为2的正三角形,DC=4,O为BD的中点,E为PA的一动点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x+4y+2=0 | B. | x+4y-2=0 | C. | x+y+2=0 | D. | x+y-2=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{e}{2}$ | B. | e | C. | e-1 | D. | $\frac{e}{2}$-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | (¬p)∧(?q) | C. | p∧(¬q) | D. | (¬p)∧q |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com