
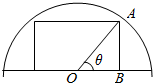
 如图所示,在一住宅小区里有一块半径为10m的半圆形空地(O为圆心),现准备在这块空地上种植一块矩形草坪,矩形的一边落在半圆的直径上,问角θ为多少度时,矩形草坪面积最大?并求出最大面积.
如图所示,在一住宅小区里有一块半径为10m的半圆形空地(O为圆心),现准备在这块空地上种植一块矩形草坪,矩形的一边落在半圆的直径上,问角θ为多少度时,矩形草坪面积最大?并求出最大面积. 分析 如图用圆的半径R与图中所示的角(可设出)表示出来,把此矩形的面积表示出来,再用三角函数的相关的公式化简,最后用三角函数的有界性判断最大值在什么情况下取到,求出矩形的最大面积以及矩形的长与宽的大小.
解答 解:由题意矩形的另两个顶点在半圆轴上时,矩形面积才能取得最大值.
设矩形在半圆板直径上的一边长为2x,θ角如图所示,
则x=10cosθ,另一边的长为10sinθ,矩形面积S为
S=200sinθcosθ.
=100sin2θ
当2θ=90°即α=45°时,也即长为20cos45°=10$\sqrt{2}$,
宽为10sin45°=5$\sqrt{2}$时,矩形面积最大
最大面积是100.
角θ为45度时,矩形草坪面积最大,最大面积为100m2.
点评 本题考查用三角函数解决实际问题的最值,这是三角函数的一个重要的运用,请仔细体会本题中函数关系的建立过程.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | P?α,l∩α=Q | B. | P∈α,l∪α=Q | C. | P∈α,l∩α=Q | D. | P?α,l∪α=Q |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 过a一定存在平面β,使得β∥α | |
| B. | 过a一定存在平面β,使得β⊥α | |
| C. | 在平面α内一定不存在直线b,使得a⊥b | |
| D. | 在平面α内一定不存在直线b,使得a∥b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com