
分析 根据题意,分析可得两名男生不能相邻,女生必须分成2组,据此分2种情况讨论:1、甲单独为一组,2、甲与一名女生分为一组,分别求出每种情况下的排法数目,由加法原理计算可得答案.
解答 解:根据题意,3位女生有且只有两位相邻,则女生必须分成2组,据此分2种情况讨论:
1、甲单独为一组,则另外2名女生为另一组,2名女生之间有2种不同的顺序,
将2名男生全排列,有A22=2种情况,排好后有3个空位,
甲只能排在两名男生中间的空位,有1种情况,两名女生的一组有2个空位可选,即有2种情况,
此时有2×2×2=8种情况,
2、甲与一名女生分为一组,需要先在2名女生中取出1人,与甲一组,有2种情况,
再分2种情况进行讨论:
将2名男生全排列,有A22=2种情况,排好后有3个空位,
①、如果甲与这名女生排在两名男生中间,有A22=2种不同的顺序,
另1名女生有2种空位可选,有2种情况,
此时有2×2×2×2=16种情况,
②、甲与这名女生不排在两名男生中间,即排在两端的空位上,只有1种顺序,
另1名女生排在两名男生中间或另一端,有2种情况,
此时有2×2×2×2=16种情况,
甲与一名女生分为一组有16+16=32种不同的排法,
综合可得:若女生甲不站两端,3位女生有且只有两位相邻,不同的排法种数为8+32=40;
故答案为:40.
点评 本题考查排列组合的运用,当题目中有限制的条件有两个,注意解题时要分清两个条件所指.


科目:高中数学 来源: 题型:选择题
| A. | 命题“若x2=1,则x=1”的否命题为“若x2=1,则x≠1” | |
| B. | 命题“?x0∈R,x${\;}_{0}^{2}$+x0-1<0”的否定是“?x∈R,x2+x-1>0” | |
| C. | 命题“若x=y,则sin x=sin y”的逆否命题为假命题 | |
| D. | 若“p或q”为真命题,则p,q中至少有一个为真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
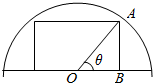 如图所示,在一住宅小区里有一块半径为10m的半圆形空地(O为圆心),现准备在这块空地上种植一块矩形草坪,矩形的一边落在半圆的直径上,问角θ为多少度时,矩形草坪面积最大?并求出最大面积.
如图所示,在一住宅小区里有一块半径为10m的半圆形空地(O为圆心),现准备在这块空地上种植一块矩形草坪,矩形的一边落在半圆的直径上,问角θ为多少度时,矩形草坪面积最大?并求出最大面积.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a2是一个有理数 | B. | a3是一个有理数 | C. | $\frac{1}{a}$是一个有理数 | D. | |a|是一个有理数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com