
已知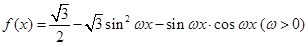 ,且
,且 图象的相邻两条对称轴间的距离为
图象的相邻两条对称轴间的距离为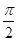 ,
,
(1)求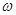 的值;
的值;
(2)求 在
在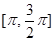 上的值域.
上的值域.
 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:解答题
某个公园有个池塘,其形状为直角△ABC,∠C=90°,AB=2百米,BC=1百米.
(1)现在准备养一批供游客观赏的鱼,分别在AB、BC、CA上取点D,E,F,如图(1),使得EF‖AB,EF⊥ED,在△DEF喂食,求△DEF 面积S△DEF的最大值;
(2)现在准备新建造一个荷塘,分别在AB,BC,CA上取点D,E,F,如图(2),建造△DEF
连廊(不考虑宽度)供游客休憩,且使△DEF为正三角形,求△DEF边长的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=2sin(ωx+ )(ω>0,0<
)(ω>0,0< <π)的图象如图所示.
<π)的图象如图所示.
(1)求函数f(x)的解析式:
(2)已知 =
= ,且a∈(0,
,且a∈(0,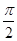 ),求f(a)的值.
),求f(a)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知 ,
, ,其中
,其中 ,若函数
,若函数 ,且函数
,且函数 的图象与直线y=2两相邻公共点间的距离为
的图象与直线y=2两相邻公共点间的距离为 .
.
(l)求 的值;
的值;
(2)在△ABC中,以a,b,c(分别是角A,B,C的对边,且 ,求△ABC周长的取值范围.
,求△ABC周长的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com