
已知函数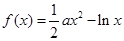 ,
,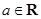 .
.
(1)求函数 的单调区间;
的单调区间;
(2)若函数 在区间
在区间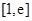 的最小值为
的最小值为 ,求
,求 的值.
的值.
(1)当 时,函数
时,函数 的单调减区间是
的单调减区间是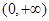 ,当
,当 时,函数
时,函数 的单调减区间是
的单调减区间是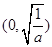 ,单调增区间为
,单调增区间为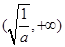 ;(2)
;(2) .
.
解析试题分析:(1)求函数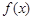 的单调区间,可利用定义,也可利用求导法,本题含有对数函数,可通过求导法来求函数
的单调区间,可利用定义,也可利用求导法,本题含有对数函数,可通过求导法来求函数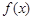 的单调区间,求函数
的单调区间,求函数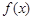 导函数
导函数 ,令
,令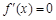 ,找出分界点,从而确定函数的单调区间,但由于含有参数
,找出分界点,从而确定函数的单调区间,但由于含有参数 ,需对参数
,需对参数 分
分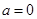 ,
, ,
, 讨论,从而得函数
讨论,从而得函数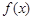 的单调区间;(2)若函数
的单调区间;(2)若函数 在区间
在区间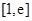 的最小值为
的最小值为 ,求
,求 的值,求出函数
的值,求出函数 在区间
在区间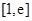 的最小值,令它等于为
的最小值,令它等于为 即可,由(1)可知,当
即可,由(1)可知,当 时,函数
时,函数 的单调减区间是
的单调减区间是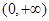 ,
, 的最小值为
的最小值为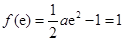 ,解出
,解出 ,验证是否符合,当
,验证是否符合,当 时,函数
时,函数 的单调减区间是
的单调减区间是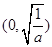 ,单调增区间为
,单调增区间为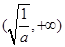 ,由于不知函数
,由于不知函数 在区间
在区间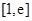 的单调性,需讨论
的单调性,需讨论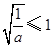 ,
, ,
,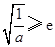 ,分别求出函数
,分别求出函数 在区间
在区间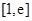 的最小值,令它等于为
的最小值,令它等于为 ,解出
,解出 ,验证是否符合,从而得
,验证是否符合,从而得 的值.
的值.
试题解析:函数 的定义域是
的定义域是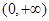 ,
, 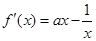
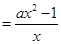 .
.
(1)(1)当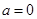 时,
时,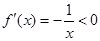 ,故函数
,故函数 在
在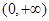 上单调递减.
上单调递减.
(2)当 时,
时,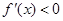 恒成立,所以函数
恒成立,所以函数 在
在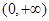 上单调递减.
上单调递减.
(3)当 时,令
时,令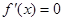 ,又因为
,又因为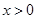 ,解得
,解得 .
.
①当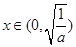 时,
时,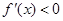 ,所以函数
,所以函数 在
在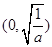 单调递减.
单调递减.
②当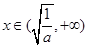 时,
时,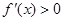 ,所以函数
,所以函数 在
在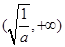 单调递增.
单调递增.
综上所述,当 时,函数
时,函数 的单调减区间是
的单调减区间是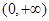 ,
,
当 时,函数
时,函数 的单调减区间是
的单调减区间是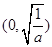 ,单调增区间为
,单调增区间为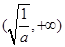 . 7分
. 7分
(2)(1)当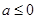 时,由(1)可知,
时,由(1)可知, 在
在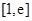 上单调递减,
上单调递减,
所以 的最小值为
的最小值为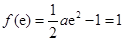 ,解得
,解得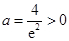 ,舍去.
,舍去.
(2)当

科目:高中数学 来源: 题型:解答题
某工厂有一批货物由海上从甲地运往乙地,已知轮船的最大航行速度为60海里/小时,甲地至乙地之间的海上航行距离为600海里,每小时的运输成本由燃料费和其他费用组成,轮船每小时的燃料费与轮船速度的平方成正比,比例系数为0.5,其余费用为每小时1250元。
(1)把全程运输成本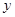 (元)表示为速度
(元)表示为速度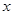 (海里/小时)的函数;
(海里/小时)的函数;
(2)为使全程运输成本最小,轮船应以多大速度行驶?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,半径为30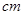 的圆形(
的圆形( 为圆心)铁皮上截取一块矩形材料
为圆心)铁皮上截取一块矩形材料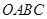 ,其中点
,其中点 在圆弧上,点
在圆弧上,点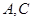 在两半径上,现将此矩形材料卷成一个以
在两半径上,现将此矩形材料卷成一个以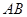 为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设
为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设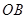 与矩形材料的边
与矩形材料的边 的夹角为
的夹角为 ,圆柱的体积为
,圆柱的体积为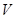
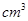 .
.
(1)求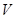 关于
关于 的函数关系式?
的函数关系式?
(2)求圆柱形罐子体积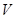 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设函数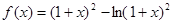 ,
,
(1)求函数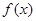 的单调区间;
的单调区间;
(2)若当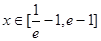 时,不等式
时,不等式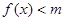 恒成立,求实数
恒成立,求实数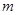 的取值范围;
的取值范围;
(3)若关于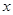 的方程
的方程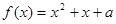 在区间
在区间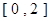 上恰好有两个相异的实根,求实数
上恰好有两个相异的实根,求实数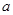 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一个圆柱形圆木的底面半径为1m,长为10m,将此圆木沿轴所在的平面剖成两个部分.现要把其中一个部分加工成直四棱柱木梁,长度保持不变,底面为等腰梯形 (如图所示,其中O为圆心,
(如图所示,其中O为圆心,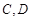 在半圆上),设
在半圆上),设 ,木梁的体积为V(单位:m3),表面积为S(单位:m2).
,木梁的体积为V(单位:m3),表面积为S(单位:m2).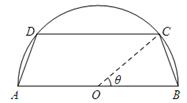
(1)求V关于θ的函数表达式;
(2)求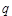 的值,使体积V最大;
的值,使体积V最大;
(3)问当木梁的体积V最大时,其表面积S是否也最大?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com