
分析 (Ⅰ)将f(sinx),f(cosx)代入f(t),分子分母分别乘以(1-sinx),(1-cosx)去掉根号,再由x的范围去绝对值可得答案.
(Ⅱ)先由x的范围求出x+$\frac{π}{4}$的范围,再由三角函数的单调性可得答案.
解答 解:(Ⅰ)由$π<x<\frac{3π}{2}$知sinx<0,cosx<0,
∴$F(x)=sinx\sqrt{\frac{1-cosx}{1+cosx}}+cosx\sqrt{\frac{1-sinx}{1+sinx}}$=$sinx•\frac{1-cosx}{|sinx|}+cosx•\frac{1-sinx}{|cosx|}$=sinx+cosx-2=$\sqrt{2}sin({x+\frac{π}{4}})-2$;
(Ⅱ)由$π<x<\frac{3π}{2}$得$\frac{5π}{4}<x+\frac{π}{4}<\frac{7π}{4}$
∴$-1≤sin({x+\frac{π}{4}})<-\frac{{\sqrt{2}}}{2}$
∴$-2-\sqrt{2}≤\sqrt{2}sin({x+\frac{π}{4}})-2<-3$
∴F(x)的值域是$[{-2-\sqrt{2},-3})$.
点评 本小题主要考查函数的定义域、值域和三角函数的性质等基本知识,考查三角恒等变换、代数式的化简变形和运算能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
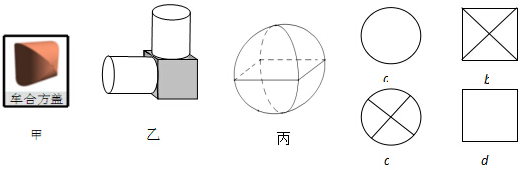
| A. | a,b | B. | a,d | C. | c,b | D. | c,d |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com