考点:其他不等式的解法
专题:计算题,不等式的解法及应用
分析:(1)不等式x
3-2x
2+3<0?(x+1)(x
2-3x+3)<0,从而可求得其解集;
(2)对不等式x(x-1)
2(x+1)
3(x+2)≥0中的x分x<-2,-2≤x≤-1,-1<x<0与x≥0四类讨论,即可求得答案;
(3)将原不等式右端的2移到左端,通分转化为
≤0,利用穿根法即可求得答案;或者转化为
| | (x-6)(2x-5)≥0 | | (x-3)(x-5)<0 |
| |
①或
| | (x-6)(2x-5)≤0 | | (x-3)(x-5)>0 |
| |
②,分别解①与②即可求得答案.
解答:
解:(1)不等式x
3-2x
2+3<0?(x+1)(x
2-3x+3)<0,
∵方程x
2-3x+3=0中,△=(-3)
2-4×3=-3<0,且首项系数大于0,
∴x
2-3x+3>0恒成立,
∴(x+1)(x
2-3x+3)<0?x+1<0,
∴x<-1,
∴不等式x
3-2x
2+3<0的解集为{x|x<-1};
(2)∵x(x-1)
2(x+1)
3(x+2)≥0,
∴当x<-2时,x+2<0,x+1<0?(x+1)
3<0,(x-1)
2>0,x<0,
∴x(x-1)
2(x+1)
3(x+2)<0,
∴x<-2不符合题意;
当-2≤x≤-1时,同理可得x(x-1)
2(x+1)
3(x+2)≥0,符合题意;
当-1<x<0时,同理可知x(x-1)
2(x+1)
3(x+2)<0,
∴-1<x<0不符合题意;
当x≥0时,x(x-1)
2(x+1)
3(x+2)≥0成立,
综上所述,不等式x(x-1)
2(x+1)
3(x+2)≥0的解集为{x|-2≤x≤-1或x≥0};
(3)∵
≥2,
∴
≥0,整理得:
≤0,
由穿根法知,
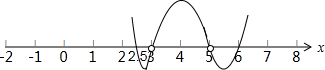
原不等式的解集为{x|
≤x<3或5<x≤6}.
或者:
≤0?
| | (x-6)(2x-5)≥0 | | (x-3)(x-5)<0 |
| |
①或
| | (x-6)(2x-5)≤0 | | (x-3)(x-5)>0 |
| |
②,
解①得x∈∅;
解②得
≤x<3或5<x≤6,
∴原不等式的解集为:{x|
≤x<3或5<x≤6}.
点评:本题考查不等式的解法,考查等价转化思想与分类讨论思想的综合应用,考查运算求解能力,属于中档题.



