
分析 (1)直线l的参数方程为$\left\{\begin{array}{l}x=1+\frac{1}{2}t\\ y=\frac{\sqrt{3}}{2}t\end{array}$ (t为参数),消去参数t得直线l的普通方程;曲线C的极坐标方程ρ2+ρ2sin2θ=2,化成直角坐标方程为x2+2y2=2;
(2)将直线l的参数方程代入曲线C:x2+2y2=2,得7t2+4t-4=0,利用参数的几何意义,即可求$\frac{1}{|AP{|}^{2}}$+$\frac{1}{|BP{|}^{2}}$.
解答 解:(1)直线l的参数方程为$\left\{\begin{array}{l}x=1+\frac{1}{2}t\\ y=\frac{\sqrt{3}}{2}t\end{array}$ (t为参数),消去参数t得直线l的普通方程为$\sqrt{3}$x-y-$\sqrt{3}$=0,
曲线C的极坐标方程ρ2+ρ2sin2θ=2,化成直角坐标方程为x2+2y2=2,即$\frac{{x}^{2}}{2}$+y2=1.(5分)
(2)将直线l的参数方程代入曲线C:x2+2y2=2,得7t2+4t-4=0.
设A,B两点在直线l的参数方程中对应的参数分别为t1,t2,
则t1+t2=-$\frac{4}{7}$,t1t2=-$\frac{4}{7}$,
∴$\frac{1}{|AP{|}^{2}}$+$\frac{1}{|BP{|}^{2}}$=$\frac{1}{|{t}_{1}{|}^{2}}$+$\frac{1}{|{t}_{2}{|}^{2}}$=$\frac{({t}_{1}+{t}_{2})^{2}-2{t}_{1}{t}_{2}}{({t}_{1}{t}_{2})^{2}}$=$\frac{9}{2}$.(12分)
点评 本题考查参数方程、极坐标方程的转化,考查参数方程的运用,考查参数的几何意义,属于中档题.


 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
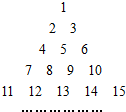 将全体正整数排成一个三角形数阵:按照如图所示排列的规律:
将全体正整数排成一个三角形数阵:按照如图所示排列的规律:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com