
【题目】已知函数f(x)=ax﹣ ![]() x2﹣aln(x+1)(a>0),g(x)=ex﹣x﹣1,曲线y=f(x)与y=g(x)在原点处的公共的切线.
x2﹣aln(x+1)(a>0),g(x)=ex﹣x﹣1,曲线y=f(x)与y=g(x)在原点处的公共的切线.
(1)若x=0为函数f(x)的极大值点,求f(x)的单调区间(用a表示);
(2)若x≥0,g(x)≥f(x)+ ![]() x2 , 求a的取值范围.
x2 , 求a的取值范围.
【答案】
(1)解:由题意得:f(x)的定义域是(﹣1,+∞),
且f′(x)=a﹣x﹣ ![]() ,g′(x)=ex﹣1,
,g′(x)=ex﹣1,
∵曲线y=f(x)与y=g(x)在原点处的公共的切线,
∴f′(0)=g′(0),
解得:a=b,
∴f(x)=ax﹣ ![]() x2﹣aln(x+1);
x2﹣aln(x+1);
f′(x)= ![]() ,
,
a=1时,f′(x)≤0,函数在定义域递减,不合题意;
a≠1时,∵x=0为函数f(x)的极大值点,
故由y=﹣x2+(a﹣1)x的图象可知a﹣1<0,
由f′(x)<0,得:x∈(﹣1,a﹣1)∪(0,+∞),
由f′(x)>0,得:x∈(a﹣1,0),
∴f(x)在(a﹣1,0)递增,在(﹣1,a﹣1),(0,+∞)递减
(2)解:∵g′(x)=ex﹣1,且﹣1<x<0时,g′(x)<0,x>0时,g′(x)>0,
故x=0时,g(x)取得最小值0,∴g′(x)≥0,即ex≥x+1,从而x≥ln(x+1),
设F(x)=g(x)﹣f(x)﹣ ![]() x2=ex+aln(x+1)﹣(a+1)x﹣1,
x2=ex+aln(x+1)﹣(a+1)x﹣1,
F′(x)=ex+ ![]() ﹣(a+1),
﹣(a+1),
①a=1时,∵x≥0,∴F′(x)≥x+1+ ![]() ﹣(a+1)=x+1+
﹣(a+1)=x+1+ ![]() ﹣2≥0,
﹣2≥0,
∴F(x)在[0,+∞)递增,从而F(x)≥F(0)=0,
即ex+ln(x+1)=2x﹣1>0,
∴g(x)≥f(x)+ ![]() x2,
x2,
②0<a<1时,由①得:ex+ln(x+1)﹣2x﹣1>0,
∴g(x)=ex﹣x﹣1≥x﹣ln(x+1)≥a(x﹣ln(x+1)),
故F(x)≥0即g(x)≥f(x)+ ![]() x2,
x2,
③a>1时,令h(x)=ex+ ![]() ﹣(a+1),
﹣(a+1),
则h′(x)=ex﹣ ![]() ,
,
显然h′(x)在[0,+∞)递增,又h′(0)=1﹣a<0,h′( ![]() ﹣1)=
﹣1)= ![]() ﹣1>0,
﹣1>0,
∴h′(x)在(0, ![]() ﹣1)上存在唯一零点x0,
﹣1)上存在唯一零点x0,
当x∈(0,x0)时,h′(x)<0,h(x)在[0,x0)递减,
x∈(0,x0)时,F(x)<F(0)=0,
即g(x)<f(x)+ ![]() x2,不合题意,
x2,不合题意,
综上,a∈(0,1].
【解析】(1)求出函数的导数,根据f′(0)=g′(0),求出a=b,求出f(x)的导数,通过讨论a的范围,确定函数的单调区间即可;(2)设F(x)=g(x)﹣f(x)﹣ ![]() x2 , 通过讨论a的范围结合函数的单调性确定a的具体范围即可.
x2 , 通过讨论a的范围结合函数的单调性确定a的具体范围即可.
【考点精析】通过灵活运用利用导数研究函数的单调性和函数的极值与导数,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值即可以解答此题.
是极小值即可以解答此题.


科目:高中数学 来源: 题型:
【题目】BD是等腰直角三角形△ABC腰AC上的中线,AM⊥BD于点M,延长AM交BC于点N,AF⊥BC于点F,AF与BD交于点E.
(1)求证;△ABE≌△ACN;
(2)求证:∠ADB=∠CDN.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的右焦点
的右焦点![]() ,过点
,过点![]() 且与坐标轴不垂直的直线与椭圆交于
且与坐标轴不垂直的直线与椭圆交于![]() ,
,![]() 两点,当直线
两点,当直线![]() 经过椭圆的一个顶点时其倾斜角恰好为
经过椭圆的一个顶点时其倾斜角恰好为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 为坐标原点,线段
为坐标原点,线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,求出实数
?若存在,求出实数![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面四边形ABCD内接于圆O,AC是圆O的一条直径,PA⊥平面ABCD,PA=AC=2,E是PC的中点,∠DAC=∠AOB 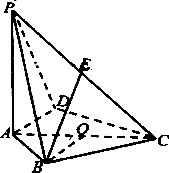
(1)求证:BE∥平面PAD;
(2)若二面角P﹣CD﹣A的正切值为2,求直线PB与平面PCD所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C1: ![]() +
+ ![]() =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为 ![]() ,其右焦点到直线2ax+by﹣
,其右焦点到直线2ax+by﹣ ![]() =0的距离为
=0的距离为 ![]() .
.
(1)求椭圆C1的方程;
(2)过点P(0,﹣ ![]() )的直线l交椭圆C1于A,B两点.
)的直线l交椭圆C1于A,B两点.
①证明:线段AB的中点G恒在椭圆C2: ![]() +
+ ![]() =1的内部;
=1的内部;
②判断以AB为直径的圆是否恒过定点?若是,求出该定点的坐标;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体ABCD-A1B1C1D1中,M、N、E、F分别是棱A1B1、A1D1、B1C1、C1D1的中点.
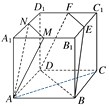
(1)求MN与AC所成角,并说明理由.
(2)求证:平面AMN∥平面EFDB.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() .
.
(1)若![]() 和
和![]() 分别是先后抛掷一枚骰子得到的点数,求对任意
分别是先后抛掷一枚骰子得到的点数,求对任意![]() ,
, ![]() 恒成立的概率;
恒成立的概率;
(2)若![]() 是从区间
是从区间![]() 任取的一个数,
任取的一个数, ![]() 是从
是从![]() 任取的一个数,求函数
任取的一个数,求函数![]() 的图像与
的图像与![]() 轴有交点的概率.
轴有交点的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2012年中华人民共和国环境保护部批准《环境空气质量标准》为国家环境质量标准,该标准增设和调整了颗粒物、二氧化氮、铅、笨等的浓度限值,并从2016年1月1日起在全国实施.空气质量的好坏由空气质量指数确定,空气质量指数越高,代表空气污染越严重,某市对市辖的某两个区加大了对空气质量的治理力度,从2015年11月1日起监测了100天的空气质量指数,并按照空气质量指数划分为:指标小于或等于115为通过,并引进项目投资.大于115为未通过,并进行治理.现统计如下.
空气质量指数 | (0,35] | [35,75] | (75,115] | (115,150] | (150,250] | >250 |
空气质量类别 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
甲区天数 | 13 | 20 | 42 | 20 | 3 | 2 |
乙区天数 | 8 | 32 | 40 | 16 | 2 | 2 |
(1)以频率值作为概率值,求甲区和乙区通过监测的概率;
(2)对于甲区,若通过,引进项目可增加税收40(百万元),若没通过监测,则治理花费5(百万元);对于乙,若通过,引进项目可增加税收50(百万元),若没通过监测,则治理花费10(百万元)..在(1)的前提下,记X为通过监测,引进项目增加的税收总额,求随机变量X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 满足:在区间
满足:在区间![]() 内有且仅有一个实数
内有且仅有一个实数![]() ,使得
,使得![]() 成立,则称函数
成立,则称函数![]() 具有性质M.
具有性质M.
![]() 判断函数
判断函数![]() 是否具有性质M,说明理由;
是否具有性质M,说明理由;
![]() 若函数
若函数![]() 具有性质M,求实数a的取值范围;
具有性质M,求实数a的取值范围;
![]() 若函数
若函数![]() 具有性质M,求实数m的取值范围.
具有性质M,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com