
分析 根据题意,先由分步计数原理计算4个人选3门课的全部情况数目,再分2步来计算其中恰有2人选修课程甲的情况数目,具体为只需先从4人中选出2人选修课程甲,再让剩余2人选乙、丙两门;由等可能事件的概率公式,计算可得答案.
解答 解:根据题意,
4位同学每人从甲、乙、丙3门课程中选修1门,4个人每人都有3种选法,
则4个人选3门课,有3×3×3×3=81种情况,
要使恰有2人选修课程甲,只需先从4人中选出2人选修课程甲,有C42=6种选法,
再让剩余2人选乙、丙两门,有2×2=4种选法,
则恰有2人选修课程甲的情况有6×4=24种;
则恰有2人选修课程甲的概率为$\frac{24}{81}$=$\frac{8}{27}$.
故答案为:$\frac{8}{27}$.
点评 本题考查等可能事件的概率计算,注意题干中并没有要求必须每一门课程必须有人选,应采用分步计数原理来计算.


科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
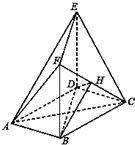 如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,H是CF的中点.
如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,H是CF的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,AB是半径为1的圆的直径,过点A,B分别引弦AD和BE,相交于点C,过点C作CF⊥AB,垂足为点F.已知∠CAB=30°,∠DCB=60°.
如图所示,AB是半径为1的圆的直径,过点A,B分别引弦AD和BE,相交于点C,过点C作CF⊥AB,垂足为点F.已知∠CAB=30°,∠DCB=60°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com