
分析 构造函数令t=$\sqrt{1+x}$+$\sqrt{1-x}$,
($\sqrt{1+x}$+$\sqrt{1-x}$)2=2+2$\sqrt{1-{x}^{2}}$=t2,通过求导,判断函数的单调性,求出函数的最值,得出m的取值范围.
解答 解:令t=$\sqrt{1+x}$+$\sqrt{1-x}$,
($\sqrt{1+x}$+$\sqrt{1-x}$)2=2+2$\sqrt{1-{x}^{2}}$=t2,
∴2$\sqrt{1-{x}^{2}}$-1=t2-3,
∴-1≤t2-3≤1,
∴$\sqrt{2}$≤t≤2,
∴f(x)=($\sqrt{1+x}$+$\sqrt{1-x}$)(2$\sqrt{1-{x}^{2}}$-1)
=t3-3t,
y'=3t2-3,
∴定义域内递增,
∴-$\sqrt{2}$≤f(x)≤2,
∵关于x的方程f(x)=m有实数解,
∴-$\sqrt{2}$≤m≤2,
故答案为-$\sqrt{2}$≤m≤2,
点评 考查了函数的构造和利用导函数求出函数的值域.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
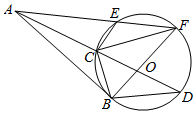 如图,AB是圆O的一条切线,切点为B,AF、AD都是圆O的割线,AD交圆O于点C,AF交圆O于点E,且∠ABC=∠ECF,连接EC、FB,BF过圆心O.
如图,AB是圆O的一条切线,切点为B,AF、AD都是圆O的割线,AD交圆O于点C,AF交圆O于点E,且∠ABC=∠ECF,连接EC、FB,BF过圆心O.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com