
| A�� | $\sqrt{5}$ | B�� | 2 | C�� | $\sqrt{3}$ | D�� | $\sqrt{2}$ |
���� ���������ߺ�˫���ߵ�λ�ù�ϵ���õ������ߵ��߷���Ϊx=-a����$\overrightarrow{{A_1}N}=\overrightarrow{M{A_2}}$����MA2��x�ᣬ�ɡ�MA1N=135�㣬��������MA1A2�ǵ���ֱ�������Σ��Ӷ��õ�b=2a��������⼴�ɣ�
��� 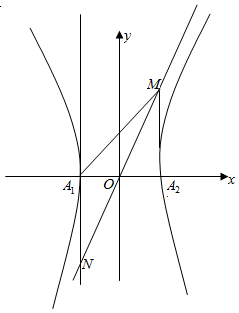 �⣺��������E������ԭ��Ϊ���㣬��A2Ϊ���㣮
�⣺��������E������ԭ��Ϊ���㣬��A2Ϊ���㣮
�������ߵ��߷���Ϊx=-a��
��$\overrightarrow{{A_1}N}=\overrightarrow{M{A_2}}$����MA2��x�ᣬ
�轥����Ϊy=$\frac{b}{a}$x����x=aʱ��y=b����M��a��b����
�ߡ�MA1N=135�㣬
���MA1A2=45�㣬
��������MA1A2�ǵ���ֱ�������Σ�
�� MA2=A1A2����b=2a��
��c=$\sqrt{{a}^{2}+{b}^{2}}$=$\sqrt{5}$a��
��������e=$\frac{c}{a}$=$\sqrt{5}$��
��ѡ��A��
���� ������Ҫ����˫���������ʵļ��㣬����˫���ߺ������ߵĹ�ϵȷ��������MA1A2�ǵ���ֱ���������ǽ������Ĺؼ���


 ����С״Ԫ��������������ϵ�д�
����С״Ԫ��������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��������ֱ��ƽ�У��Ҿ������6cm��һ��ֱ�� | |
| B�� | ��������ֱ��ƽ�У��Ҿ������3cm������ֱ�� | |
| C�� | ��������ֱ��ƽ�У��Ҿ������3cm��һ��ֱ�� | |
| D�� | ��������ֱ��ƽ�У��Ҿ������3cm������ֱ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{\sqrt{2}+\sqrt{6}}{2}$ | B�� | $\frac{\sqrt{2}-\sqrt{6}}{2}$ | C�� | $\frac{\sqrt{2}+\sqrt{6}}{4}$ | D�� | $\frac{\sqrt{2}-\sqrt{6}}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | $\sqrt{2}$ | C�� | 1 | D�� | $\frac{{\sqrt{2}}}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
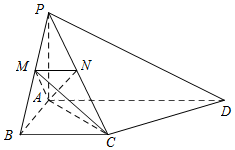 ��ͼ��PA��ƽ��ABCD��AB��AD��AD��BC��PA=AB=BC��AD=2AB����M��N�ֱ���PB��PC�ϣ���MN��BC��
��ͼ��PA��ƽ��ABCD��AB��AD��AD��BC��PA=AB=BC��AD=2AB����M��N�ֱ���PB��PC�ϣ���MN��BC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{5}$ | B�� | 2 | C�� | $\sqrt{3}$ | D�� | $\sqrt{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com