
分析 由f(x)为奇函数便有f(-x)=-f(x),即得到$lo{g}_{2}(-2x+\sqrt{4{x}^{2}+3t})$=$-lo{g}_{2}(2x+\sqrt{4{x}^{2}+3t})$,分子有理化并进行对数的运算便可得到$lo{g}_{2}(3t)-lo{g}_{2}(2x+\sqrt{4{x}^{2}+3t})$=$-lo{g}_{2}(2x+\sqrt{4{x}^{2}+3t})$,这样便可得出3t=1,从而求出实数t的值.
解答 解:f(x)为奇函数;
∴f(-x)=-f(x);
即$lo{g}_{2}(-2x+\sqrt{4{x}^{2}+3t})=lo{g}_{2}\frac{3t}{2x+\sqrt{4{x}^{2}+3t}}$=$lo{g}_{2}3t-lo{g}_{2}(2x+\sqrt{4{x}^{2}+3t})=-lo{g}_{2}(2x+\sqrt{4{x}^{2}+3t})$;
∴log2(3t)=0;
∴3t=1;
∴$t=\frac{1}{3}$.
故答案为:$\frac{1}{3}$.
点评 本题考查奇函数的定义,分子有理化和平方差公式,以及对数的运算.


 高中必刷题系列答案
高中必刷题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (4,+∞) | B. | [0,$\frac{1}{2}$] | C. | ($\frac{1}{2}$,4] | D. | (1,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
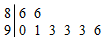 如图是某班8为学生诗词比赛得分的茎叶图,那么这8为学生得分的众数和中位数分别为( )
如图是某班8为学生诗词比赛得分的茎叶图,那么这8为学生得分的众数和中位数分别为( )| A. | 93,91 | B. | 86,93 | C. | 93,92 | D. | 86,91 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 完成时间 | 频率 |
| [20,25) | 0.2 |
| [25,30) | 0.5 |
| [30,35) | 0.2 |
| [35,40) | 0.1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com