练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
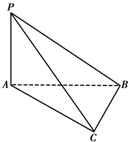
    如图所示，已知PA垂直于△ABC所在平面，且∠ACB=90°，连结PB、PC，则图形中互相垂直的平面有（　　）
    A、一对B、两对C、三对D、四对
    考点：平面与平面垂直的判定
    专题：空间位置关系与距离
    分析：由PA垂直于△ABC所在平面，得到平面PAB⊥平面ABC，平面PAC⊥平面ABC，由线面垂直得PA⊥BC，又∠ACB=90°，所以BC⊥平面PAC，由此得平面PBC⊥平面PAC，故图形中互相垂直的平面有3对．
    解答： 解：∵PA垂直于△ABC所在平面，连结PB、PC，
    ∵PA?平面PAB，∴平面PAB⊥平面ABC，
    又∵PA?平面PAC，∴平面PAC⊥平面ABC，
    ∵PA垂直于△ABC所在平面，
    ∴PA⊥BC，又∠ACB=90°，∴BC⊥AC，
    ∴BC⊥平面PAC，
    ∵BC?平面PBC，
    ∴平面PBC⊥平面PAC．
    ∴图形中互相垂直的平面有3对．
    故选：C．
    点评：本题考查平面与平面垂直的判断，是基础题，解题时要注意空间思维能力的培养．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

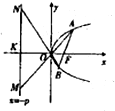    如图，过抛物线C：y2=2px的焦点F与x轴不垂直的直线交抛物线C与A、B两点，直线AO、BO分别与直线m：x=-p相交于M、N两点，则
    S△ABO
    S△MNO
    =（　　）
    A、1
    B、
    1
    2
    C、
    1
    4
    D、
    1
    8

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    某工厂为了对新研发的一种产品进行合理定价，将该产品按事先拟定的价格进行试销，得到数据如表．预计在今后的销售中，销量与单价仍然服从
    y
    =bx+a（ b=-20，a=
    .
    y
    -b
    .
    x
    ）的关系，且该产品的成本是4元/件，为使工厂获得最大利润（利润=销售收入-成本），该产品的单价应定为（　　）元．
    单价x（元）88.28.48.68.89
    销量y（件）908483807568
    A、
    31
    4
    B、8
    C、
    33
    4
    D、
    35
    4

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    以下判断正确的是（　　）
    A、函数y=f（x）为R上的可导函数，则f′（x0）=0是x0为函数f（x）极值点的充要条件
    B、命题“存在x∈R，x2+x-1＜0”的否定是“任意x∈R，x2+x-1＞0”
    C、“b=0”是“函数f（x）=ax2+bx+c是偶函数”的充要条件
    D、命题“在△ABC中，若A＞B，则sinA＞sinB”的逆命题为假命题

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    令P（x）：ax2+3x+2＞0，若对任意x∈R，P（x）是真命题，则实数a的取值范围是（　　）
    A、a＞0
    B、a＞
    9
    8
    C、a＜0
    D、a=0

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    将编号为1，2，3，4，5，6的六个小球排成一列，要求1号球与2号球必须相邻，4号球、5号球、6号球互不相邻，则不同的排法种数有（　　）
    A、4B、24C、72D、144

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知m，n是不同的直线，α，β是不重合的平面，下列命题正确的是（　　）：
    A、若m∥α，则m平行于平面α内的任意一条直线
    B、若α∥β，m?α，n?β，则m∥n
    C、若α∥β，m?α，则m∥β．
    D、若m?α，n?α，m∥β，n∥β，则α∥β

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    调查某医院某段时间内婴儿出生的时间与性别的关系，得到下面的数据表：
    晚上白天合计
    男婴502575
    女婴101525
    合计6040100
    （参考数据和公式见卷首）你认为婴儿的性别与出生时间有关系的把握为（　　）
    A、80%B、90%
    C、95%D、97.5%

    查看答案和解析>>

    科目：高中数学 来源： 题型：

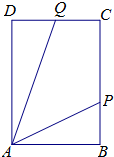    如图，ABCD是长方形海域，其中AB=10海里，AD=10
    		2
    海里．现有一架飞机在该海域失事，两艘海事搜救船在A处同时出发，沿直线AP、AQ向前联合搜索，且∠PAQ=
    π
    4
    （其中P、Q分别在边BC、CD上），搜索区域为平面四边形APCQ围成的海平面．设∠PAB=θ，搜索区域的面积为S． 
    （1）试建立S与tanθ的关系式，并指出tanθ的取值范围；
    （2）求S的最大值，并指出此时θ的值．

    查看答案和解析>>

    同步练习册答案