
分析 (Ⅰ)由ρ=x2+y2、ρcosθ=x、ρsinθ=y,将曲线C1的方程:ρ=2cosθ+2sinθ化为直角坐标方程;
(Ⅱ)将直线C2的参数方程消去t化为直角坐标方程,利用点到直线的距离求出圆心C1(1,1)到直线C2的距离d,判断出直线与圆的位置关系,即可求出答案.
解答 解:(Ⅰ)因为曲线C1的方程为ρ=2cosθ+2sinθ,则ρ2=2ρcosθ+2ρsinθ,
所以C1的直角坐标方程是x2+y2=2x+2y,即(x-1)2+(y-1)2=2;
(Ⅱ)因为直线C2的参数方程为$\left\{\begin{array}{l}{x=-1+t}\\{y=-1-t}\end{array}\right.$(t为参数)
所以直线C2的直角坐标方程为x+y+2=0,
因为圆心C1(1,1)到直线C2的距离d=$\frac{|1+1+2|}{\sqrt{2}}$=2$\sqrt{2}$$>\sqrt{2}$,
则直线与圆相离,
所以求P到直线C2的距离的最大值是3$\sqrt{2}$,最小值$\sqrt{2}$.
点评 本题考查极坐标方程及参数方程化为直角坐标方程,点到直线的距离公式,以及直线与圆的位置关系,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
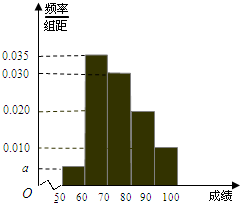 某校100名学生期中考试数学成绩的频率分布直方图如图,其中成绩分组区间如下:
某校100名学生期中考试数学成绩的频率分布直方图如图,其中成绩分组区间如下:| 组号 | 第一组 | 第二组 | 第三组 | 第四组 | 第五组 |
| 分组 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,3) | B. | (1,5) | C. | (2,3) | D. | (2,5) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 垂心 | B. | 外心 | C. | 内心 | D. | 重心 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com