
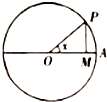
 如图,圆O的半径为1,A是圆上的定点,P是圆上的动点,角x的始边为射线OA,终边为射线OP,过点P作直线OA的垂线,垂足为M,将点M到直线OP的距离与O到M的距离之和表示成x的函数f(x),则y=f(x)在[0,π]上的图象大致是( )
如图,圆O的半径为1,A是圆上的定点,P是圆上的动点,角x的始边为射线OA,终边为射线OP,过点P作直线OA的垂线,垂足为M,将点M到直线OP的距离与O到M的距离之和表示成x的函数f(x),则y=f(x)在[0,π]上的图象大致是( )| A. | 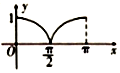 | B. | 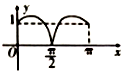 | C. | 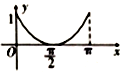 | D. | 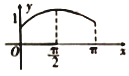 |
分析 当x∈[0,$\frac{π}{2}$]时,点M到直线OP的距离与O到M的距离之和f(x)=sinxcosx+cosx=$\frac{1}{2}$sin2x+cosx,求导分析函数的单调性,可得函数图象的大致形状,进而得到答案.
解答 解:∵圆O的半径为1,A是圆上的定点,P是圆上的动点,
角x的始边为射线OA,终边为射线OP,
过点P作直线OA的垂线,垂足为M,
当x∈[0,$\frac{π}{2}$]时,
则点M到直线OP的距离与O到M的距离之和f(x)=sinxcosx+cosx=$\frac{1}{2}$sin2x+cosx,
∵f′(x)=cos2x-sinx=-2sin2x-sinx+1=-2(sinx+$\frac{1}{4}$)2+$\frac{9}{8}$,
故当sinx<$\frac{1}{2}$,即x∈[0,$\frac{π}{6}$)时,f′(x)>0,函数为增函数,
当sinx>$\frac{1}{2}$,即x∈($\frac{π}{6}$,$\frac{π}{2}$]时,f′(x)<0,函数为减函数,
同理,x∈[$\frac{π}{2}$,$\frac{5π}{6}$)时,f′(x)>0,函数为增函数,
x∈($\frac{5π}{6}$,π]时,f′(x)<0,函数为减函数,
故选:B
点评 本题考查的知识点是函数的图象,利用导数研究函数的单调性,难度中档.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 一条直线和x轴的正方向所成的正角,叫做这条直线的倾斜角 | |
| B. | 直线的倾斜角α的取值范围是第一或第二象限角 | |
| C. | 和x轴平行的直线,它的倾斜角为180○ | |
| D. | 每一条直线都是存在倾斜角,但并非每一条直线都存在斜率 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2019,-2016) | B. | (-2019,2016) | C. | (-2019,+∞) | D. | (-∞,-2019) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2种 | B. | 10种 | C. | 12种 | D. | 14种 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{n}{n+1}$ | B. | $\frac{2n}{n+1}$ | C. | $\frac{n+1}{n+2}$ | D. | $\frac{2n}{n+2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com