Question

6．在△ABC中，AB=14cm，$\frac{AD}{BD}$=$\frac{5}{9}$，DE∥BC，CD⊥AB，CD=12cm，求△ABC的面积和周长．

Answer 1

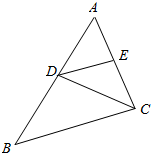
分析 由AB=14cm，CD=12cm得S_△ABC=84，利用勾股定理求出BC、AC，求△ABC的周长．

解答 解：∵在△ABC中，AB=14cm，CD⊥AB，CD=12cm，
∴S_△ABC=$\frac{1}{2}$AB•CD=$\frac{1}{2}$×14×12=84（cm²），
∵$\frac{AD}{BD}$=$\frac{5}{9}$，∴AD：AB=5：14，
∴BD=AB-AD=9cm，
∴在Rt△ACD中，AC=13（cm），
在Rt△BCD中，BC=15（cm），
∴△ABC的周长为：AB+AC+BC=42（cm）．

点评 此题考查了平行线性质以及勾股定理．此题难度适中，注意掌握数形结合思想的应用．