练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    11．某公共汽车站每隔10分钟有一辆汽车到达，乘客到达车站的时刻是任意的，则一个乘客候车时间不超过7分钟的概率是（　　）
    A．$\frac{1}{10}$B．$\frac{3}{10}$C．$\frac{5}{10}$D．$\frac{7}{10}$

    分析 由乘客到达车站的时刻是任意的知这是一个几何概型，公共汽车站每隔10分钟有一辆汽车到达知事件总数包含的时间长度是10，而满足一个乘客候车时间不超过7分钟的事件包含的时间长度是7，代入几何概型公式解答．

    解答 解：由题意本题是几何概型，
    ∵公共汽车站每隔10分钟有一辆汽车到达，
    ∴事件总数包含的时间长度是10，
    ∵乘客到达车站的时刻是任意的，
    ∴满足一个乘客候车时间不超过7分钟的事件包含的时间长度是7，
    由几何概型公式得到P=$\frac{7}{10}$；
    故选：D．

    点评 本题考查了几何概型的概率求法‘解答本题的关键是首先明确概率模型，然后选择正确的事件集合的测度，概率要通过长度、面积或体积之比来得到．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    6．若实数x，y满足${log_3}[2{cos^2}（xy）+\frac{1}{{8{{cos}^2}（xy）}}]-lny+\frac{y}{3}-ln\frac{e}{3}$=0，其中e为自然对数的底数，则（cos6x）y的值为-$\frac{1}{8}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．已知函数f（x）=cos（$\frac{4π}{3}$-2x）+2cos2x
    （1）求f（x）的最大值，并写出使f（x）取得最大值时对应的x的集合．
    （2）若把函数f（x）的图象向右平移$\frac{π}{4}$个单位长度后得到函数g（x）的图象，求函数g（x）的单调递减区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．已知圆C：x2+y2-4x+2y+2=0与直线l：3x-4y-1=0，解答下列问题：
    （1）求圆心坐标与半径；
    （2）判断圆C与直线l之间的位置关系．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．在△ABC中，AB=14cm，$\frac{AD}{BD}$=$\frac{5}{9}$，DE∥BC，CD⊥AB，CD=12cm，求△ABC的面积和周长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．已知幂函数f（x）=x${\;}^{-{k}^{2}+k+2}$k（∈Z） 满足f（2）＜f（3）
    （1）求f（x）的解析式；
    （2）若函数g（x）=1-qf（x）+（2q-1）x在区间[-1，2]上是减函数，求非负实数q的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

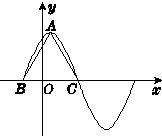    3．函数f（x）=3cosωx+$\sqrt{3}$sinωx（ω＞0）在一个周期内的图象如图所示，A为图象的最高点．B、C为图象与x轴的交点，且△ABC为正三角形．
    （1）求ω的值及f（x）的值域；
    （2）若f（x0）=$\frac{{8\sqrt{3}}}{5}$，且x0∈（-$\frac{10}{3}$，$\frac{2}{3}$），求f（x0+1）的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．甲、乙、丙三人到三个景点旅游，每人只去一个景点，设事件A为“三个人去的景点不相同”，事件B为“甲独自去一个景点”，则概率P（A|B）等于（　　）
    A．$\frac{4}{9}$B．$\frac{2}{9}$C．$\frac{1}{2}$D．$\frac{1}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．设△ABC的内角A、B、C所对的边分别为a、b、c，a=4，b=2，cosC=$\frac{1}{4}$．
    （1）求△ABC的周长；
    （2）求cos（B-C）的值．

    查看答案和解析>>

    同步练习册答案