
| A. | 42 | B. | -42 | C. | 24 | D. | -24 |
分析 写出(x-$\frac{1}{x}$)8的通项,求出其展开式中的常数项和含x-2的项,分别与1、2x2相乘后作和得答案.
解答 解:(x-$\frac{1}{x}$)8的通项${T}_{r+1}={C}_{8}^{r}{x}^{8-r}(-\frac{1}{x})^{r}=(-1)^{r}{C}_{8}^{r}{x}^{8-2r}$.
由8-2r=0,得r=4,即(x-$\frac{1}{x}$)8的常数项为${C}_{8}^{4}$;
由8-2r=-2,得r=5,即(x-$\frac{1}{x}$)8的含x-2的项为$-{C}_{8}^{5}{x}^{-2}$.
∴(1+2x2)(x-$\frac{1}{x}$)8的展开式中常数项为$1×{C}_{8}^{4}-2×{C}_{8}^{5}=-42$.
故选:B.
点评 本题考查二项式系数的性质,关键是熟记二项展开式的通项,是基础题.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | $-\sqrt{3}$ | C. | 3 | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{π}{4}$个单位长度 | B. | 向右平移$\frac{π}{4}$个单位长度 | ||
| C. | 向左平移$\frac{π}{8}$个单位长度 | D. | 向右平移$\frac{π}{8}$个单位长度 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
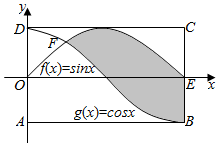 如图,矩形ABCD的四个顶点的坐标分别为A(0,-1),B(π,-1),C(π,1),D(0,1),正弦曲线f(x)=sinx和余弦曲线g(x)=cosx在矩形ABCD内交于点F,则图中阴影部分的面积为( )
如图,矩形ABCD的四个顶点的坐标分别为A(0,-1),B(π,-1),C(π,1),D(0,1),正弦曲线f(x)=sinx和余弦曲线g(x)=cosx在矩形ABCD内交于点F,则图中阴影部分的面积为( )| A. | $\sqrt{2}$+1 | B. | $\sqrt{2}$-1 | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com