Question

15．△ABC的外接圆圆心为O，半径为2，$\overrightarrow{OA}$+$\overrightarrow{AB}$+$\overrightarrow{AC}$为零向量，且|${\overrightarrow{OA}}$|=|${\overrightarrow{AB}}$|．则$\overrightarrow{CA}$在$\overrightarrow{BC}$方向上的投影为（　　）

• A． -3
• B． $-\sqrt{3}$
• C． 3
• D． $\sqrt{3}$

Answer 1

分析 根据条件容易得到$\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{OA}$，再根据O为△ABC的外心，从而得到OA，BC互相垂直平分，从而四边形OBAC为菱形，进而可得出AC=2，∠ACB=30°，这样由一个向量在另一个向量方向上投影的计算公式即可得出所求投影的值．

解答 解：$\overrightarrow{OA}+\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{OB}+\overrightarrow{OC}-\overrightarrow{OA}=\overrightarrow{0}$；
∴$\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{OA}$；
又O为△ABC的外心；
∴OA⊥BC，且OA平分BC；
∴OA，BC互相垂直平分，连接OB，OC，则四边形OBAC为菱形，如图所示：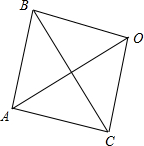

则AC=OA=2，∠ACB=30°；
∴$\overrightarrow{CA}$在$\overrightarrow{BC}$方向上的投影为$|\overrightarrow{CA}|cos＜\overrightarrow{CA}，\overrightarrow{BC}＞=2cos150°=-\sqrt{3}$．
故选：B．

点评 考查三角形外接圆及外心的概念，向量加法、减法的几何意义，以及向量的数乘运算，向量加法的平行四边形法则，菱形的概念，菱形对角线的性质，一个向量在另一个向量方向上投影的定义及计算公式．