
 如图:⊙O的直径AB的延长线于弦CD的延长线相交于点P,E为⊙O上一点,$\widehat{AE}$=$\widehat{AC}$,DE交AB于点F.
如图:⊙O的直径AB的延长线于弦CD的延长线相交于点P,E为⊙O上一点,$\widehat{AE}$=$\widehat{AC}$,DE交AB于点F.分析 (1)连接OC,OE,证明∠AOC=∠CDE,可得O,C,D,F四点共圆;
(2)利用割线定理,结合△PDF∽△POC,即可证明PF•PO=PA•PB.
解答 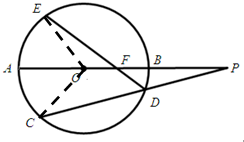 证明:(1)连接OC,OE,
证明:(1)连接OC,OE,
因为$\widehat{AE}$=$\widehat{AC}$,所以∠AOC=∠AOE=$\frac{1}{2}$∠COE,…(2分)
又因为∠CDE=$\frac{1}{2}$∠COE,
则∠AOC=∠CDE,
所以O,C,D,F四点共圆.…(5分)
(2)因为PBA和PDC是⊙O的两条割线,
所以PD•DC=PA•PB,…(7分)
因为O,C,D,F四点共圆,
所以∠PDF=∠POC,
又因为∠DPF=∠OPC,
则△PDF∽△POC,
所以$\frac{PD}{PO}=\frac{PF}{PC}$,即PF•PO=PD•PC,
则PF•PO=PA•PB.…(10分)
点评 本题考查四点共圆,考查割线定理,三角形相似的性质,考查学生分析解决问题的能力,比较基础.


科目:高中数学 来源: 题型:解答题
| 分组编号 | 年龄分组 | 球迷 | 所占比例 |
| 1 | [20,25] | 1200 | 0.5 |
| 2 | [25,30] | 1800 | 0.6 |
| 3 | [30,35] | 1000 | 0.5 |
| 4 | [35,40] | a | 0.4 |
| 5 | [40,45] | 300 | 0.2 |
| 6 | [45,50] | 200 | 0.1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3\sqrt{2}}{8}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{5\sqrt{2}}{8}$ | D. | $\frac{3\sqrt{2}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
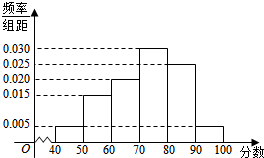 某校对参加高校自主招生测试的学生进行模拟训练,从中抽出N名学生,其数学成绩的频率分布直方图如图所示.已知成绩在区间[90,100]内的学生人数为2人.
某校对参加高校自主招生测试的学生进行模拟训练,从中抽出N名学生,其数学成绩的频率分布直方图如图所示.已知成绩在区间[90,100]内的学生人数为2人.查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 Rt△ABC中,∠C=90°,CD⊥AB,AD为圆O的直径,圆O与AC交于E,求证:$\frac{AE}{CE}$=$\frac{A{C}^{2}}{B{C}^{2}}$.
Rt△ABC中,∠C=90°,CD⊥AB,AD为圆O的直径,圆O与AC交于E,求证:$\frac{AE}{CE}$=$\frac{A{C}^{2}}{B{C}^{2}}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (0,2) | C. | (1,+∞) | D. | (2,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com