
| A. | $\frac{3\sqrt{2}}{8}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{5\sqrt{2}}{8}$ | D. | $\frac{3\sqrt{2}}{4}$ |
分析 由sinπx=cosπx=sin($\frac{π}{2}-πx$),x∈[0,2],可解得πx=$\frac{π}{2}-πx$+2kπ,k∈Z,可解得坐标:A($\frac{1}{4}$,$\frac{\sqrt{2}}{2}$),B($\frac{5}{4}$,-$\frac{\sqrt{2}}{2}$),求得直线AB所在的方程为:y-$\frac{\sqrt{2}}{2}$=-$\sqrt{2}$(x-$\frac{1}{4}$),联立方程y=0,可解得OC=$\frac{3}{4}$,即可求得△OAB面积.
解答  解:如图所示:∵sinπx=cosπx=sin($\frac{π}{2}-πx$),x∈[0,2],
解:如图所示:∵sinπx=cosπx=sin($\frac{π}{2}-πx$),x∈[0,2],
∴可解得:πx=π-($\frac{π}{2}-πx$)+2kπ,k∈Z(无解),或πx=$\frac{π}{2}-πx$+2kπ,k∈Z
∴可解得:x=$\frac{1}{4}$+k,k∈Z,且x∈[0,2],
∴x=$\frac{1}{4}$,或$\frac{5}{4}$,
∴解得坐标:A($\frac{1}{4}$,$\frac{\sqrt{2}}{2}$),B($\frac{5}{4}$,-$\frac{\sqrt{2}}{2}$).
∴解得直线AB所在的方程为:y-$\frac{\sqrt{2}}{2}$=-$\sqrt{2}$(x-$\frac{1}{4}$),联立方程y=0,可解得:x=$\frac{3}{4}$,及OC=$\frac{3}{4}$.
∴S△OAB=S△OAC+S△COB=$\frac{1}{2}×OC×\frac{\sqrt{2}}{2}+\frac{1}{2}×OC×\frac{\sqrt{2}}{2}$=$\frac{3\sqrt{2}}{8}$.
故选:A.
点评 本题主要考查了正弦函数,余弦函数的图象和性质,考查了直线的方程与三角形面积的求法,综合性较强,考查了数形结合能力和转化思想,属于中档题.


 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三棱锥P-ABC中,△ABC是边长为2的正三角形,∠PCA=90°,E,H分别为AP,AC的中点,AP=4,BE=$\sqrt{3}$.
如图,在三棱锥P-ABC中,△ABC是边长为2的正三角形,∠PCA=90°,E,H分别为AP,AC的中点,AP=4,BE=$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图:⊙O的直径AB的延长线于弦CD的延长线相交于点P,E为⊙O上一点,$\widehat{AE}$=$\widehat{AC}$,DE交AB于点F.
如图:⊙O的直径AB的延长线于弦CD的延长线相交于点P,E为⊙O上一点,$\widehat{AE}$=$\widehat{AC}$,DE交AB于点F.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
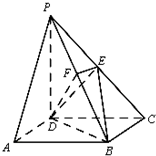 如图所示,在四棱锥P-ABCD中,底面ABCD是矩形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
如图所示,在四棱锥P-ABCD中,底面ABCD是矩形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com