
 如图,在三棱锥P-ABC中,△ABC是边长为2的正三角形,∠PCA=90°,E,H分别为AP,AC的中点,AP=4,BE=$\sqrt{3}$.
如图,在三棱锥P-ABC中,△ABC是边长为2的正三角形,∠PCA=90°,E,H分别为AP,AC的中点,AP=4,BE=$\sqrt{3}$.分析 (Ⅰ)证明:BH⊥AC,EH⊥AC,即可证明AC⊥平面BEH;
(Ⅱ)取BH得中点G,连接AG,证明∠EAG为PA与平面ABC所成的角,即可求直线PA与平面ABC所成角的正弦值.
解答 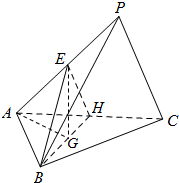 (Ⅰ)证明:因为△ABC是边长为2的正三角形,
(Ⅰ)证明:因为△ABC是边长为2的正三角形,
所以BH⊥AC.…(2分)
又因为E,H分别为AP,AC的中点,得EH∥PC,
因为∠PCA=90°,
所以EH⊥AC.…(5分)
故AC⊥平面BEH.…(7分)
(Ⅱ)解:取BH得中点G,连接AG.…(9分)
因为EH=BH=BE=$\sqrt{3}$,所以EG⊥BH.
又因为AC⊥平面BEH,所以EG⊥AC,
所以EG⊥平面ABC.
所以∠EAG为PA与平面ABC所成的角.…(12分)
在直角三角形EAG中,AE=2,EG=$\frac{3}{2}$,
所以\sin∠EAG=$\frac{EG}{EA}$=$\frac{3}{4}$.…(15分)
所以PA与平面ABC所成的角的正弦值为$\frac{3}{4}$.
点评 本题考查线面垂直的判定,考查线面角,考查学生分析解决问题的能力,正确利用线面垂直的判定定理是关键.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:解答题
 已知抛物线C:y2=2px(p>0),半圆M:x2+2x+y2=0(y≥0),过点P(-3,0)与半圆M相切于点A的直线l,与抛物线C有且只有一个公共点B.
已知抛物线C:y2=2px(p>0),半圆M:x2+2x+y2=0(y≥0),过点P(-3,0)与半圆M相切于点A的直线l,与抛物线C有且只有一个公共点B.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m∥α,m∥β,则α∥β | B. | 若m∥α,m∥n,则n∥α | C. | 若m⊥α,m∥β,则α⊥β | D. | 若m∥α,n?α,则m∥n |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3\sqrt{2}}{8}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{5\sqrt{2}}{8}$ | D. | $\frac{3\sqrt{2}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
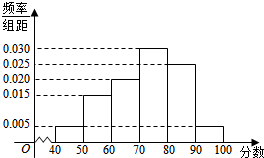 某校对参加高校自主招生测试的学生进行模拟训练,从中抽出N名学生,其数学成绩的频率分布直方图如图所示.已知成绩在区间[90,100]内的学生人数为2人.
某校对参加高校自主招生测试的学生进行模拟训练,从中抽出N名学生,其数学成绩的频率分布直方图如图所示.已知成绩在区间[90,100]内的学生人数为2人.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 Rt△ABC中,∠C=90°,CD⊥AB,AD为圆O的直径,圆O与AC交于E,求证:$\frac{AE}{CE}$=$\frac{A{C}^{2}}{B{C}^{2}}$.
Rt△ABC中,∠C=90°,CD⊥AB,AD为圆O的直径,圆O与AC交于E,求证:$\frac{AE}{CE}$=$\frac{A{C}^{2}}{B{C}^{2}}$.查看答案和解析>>
科目:高中数学 来源:2017届河南商丘第一高级中学年高三上理开学摸底数学试卷(解析版) 题型:选择题
将函数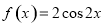 的图象向右平移
的图象向右平移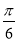 个单位后得到函数
个单位后得到函数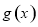 的图象.若函数
的图象.若函数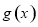 在区间
在区间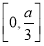 和
和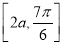 上均单调递增,则实数
上均单调递增,则实数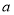 的取值范围是( )
的取值范围是( )
A. B.
B.
C.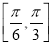 D.
D.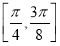
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com