
【题目】如图,几何体ABCDE中,△ABC是正三角形,EA和DC都垂直于平面ABC,且EA=AB=2a,DC=a,F、G分别为EB和AB的中点. 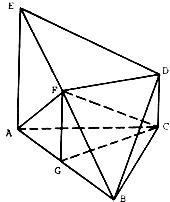
(1)求证:FD∥平面ABC;
(2)求二面角B﹣FC﹣G的正切值.
【答案】
(1)证明:连CG,FG,则四边形DEGC是平行四边形,得到DF∥CG
DF平面ABC,CG平面ABC
所以FD∥平面ABC;
(2)解:设二面角B﹣FC﹣G的大小为α
易知BG⊥平面FCG,所以△FCG为△BFC的射影
∴cosα= ![]()
∴tanα= ![]()
【解析】(1)连CG,FG,由已知中F是BE的中点,结合三角形中位线的性质,可得FG平行且等于AE的一半,又由EA、CD都垂直于平面ABC,且EA=2a,DC=a,可得四边形DEGC是平行四边形,进而得到DF∥CG,由线面平行的判定定理即可得到FD∥平面ABC;(2)易知BG⊥平面FCG,所以△FCG为△BFC的射影,故分别计算面积可求二面角的余弦值,从而得解.


 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且满足Sn=n2﹣4n,数列{bn}中,b1= ![]() 对任意正整数
对任意正整数 ![]() .
.
(1)求数列{an}的通项公式;
(2)是否存在实数μ,使得数列{3nbn+μ}是等比数列?若存在,请求出实数μ及公比q的值,若不存在,请说明理由;
(3)求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场为了了解毛衣的月销售量y(件)与月平均气温x(℃)之间的关系,随机统计了某4个月的月销售量与当月平均气温,其数据如下表:
月平均气温x(℃) | 17 | 13 | 8 | 2 |
月销售量y(件) | 24 | 33 | 40 | 55 |
由表中数据算出线性回归方程 ![]() =bx+a中的b=﹣2,气象部门预测下个月的平均气温约为6℃,据此估计该商场下个月毛衣销售量约为( )件.
=bx+a中的b=﹣2,气象部门预测下个月的平均气温约为6℃,据此估计该商场下个月毛衣销售量约为( )件.
A.46
B.40
C.38
D.58
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体 ![]() 的棱线长为
的棱线长为 ![]() ,线段
,线段 ![]() 上有两个动点
上有两个动点 ![]() ,
, ![]() ,且
,且 ![]() ,则下列结论中错误的是( ).
,则下列结论中错误的是( ).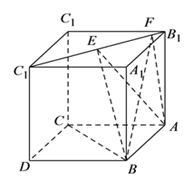
A.![]()
B.![]() 平面
平面 ![]()
C.三棱锥 ![]() 的体积为定值
的体积为定值
D.![]() 的面积与
的面积与 ![]() 的面积相等
的面积相等
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F1、F2分别为椭圆C: ![]() +
+ ![]() =1(a>b>0)的左、右焦点,且离心率为
=1(a>b>0)的左、右焦点,且离心率为 ![]() ,点A(﹣
,点A(﹣ ![]() ,
, ![]() )在椭圆C上.
)在椭圆C上.
(1)求椭圆C的方程;
(2)是否存在斜率为k的直线l与椭圆C交于不同的两点M、N,使直线F2M与F2N的倾斜角互补,且直线l是否恒过定点,若存在,求出该定点的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C所对的边分别为a,b,c.向量 ![]() =(a,
=(a, ![]() b)与
b)与 ![]() =(cosA,sinB)平行. (Ⅰ)求A;
=(cosA,sinB)平行. (Ⅰ)求A;
(Ⅱ)若a= ![]() ,b=2,求△ABC的面积.
,b=2,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() (a≠0,b∈R,c>0),g(x)=m[f(x)]2﹣n(mn>0),给出下列四个命题: ①当b=0时,函数f(x)在(0,
(a≠0,b∈R,c>0),g(x)=m[f(x)]2﹣n(mn>0),给出下列四个命题: ①当b=0时,函数f(x)在(0, ![]() )上单调递增,在(
)上单调递增,在( ![]() ,+∞)上单调递减;
,+∞)上单调递减;
②函数f(x)的图象关于x轴上某点成中心对称;
③存在实数p和q,使得p≤f(x)≤q对于任意的实数x恒成立;
④关于x的方程g(x)=0的解集可能为{﹣3,﹣1,0,1}.
则正确命题的序号为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com