
【题目】某商场为了了解毛衣的月销售量y(件)与月平均气温x(℃)之间的关系,随机统计了某4个月的月销售量与当月平均气温,其数据如下表:
月平均气温x(℃) | 17 | 13 | 8 | 2 |
月销售量y(件) | 24 | 33 | 40 | 55 |
由表中数据算出线性回归方程 ![]() =bx+a中的b=﹣2,气象部门预测下个月的平均气温约为6℃,据此估计该商场下个月毛衣销售量约为( )件.
=bx+a中的b=﹣2,气象部门预测下个月的平均气温约为6℃,据此估计该商场下个月毛衣销售量约为( )件.
A.46
B.40
C.38
D.58
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:
【题目】已知一条曲线C在y轴右边,C上每一点到点F(1,0)的距离减去它到y轴距离的差都是1.
(1)求曲线C的方程;
(2)是否存在正数m,对于过点M(m,0)且与曲线C有两个交点A,B的任一直线,都有 ![]() <0?若存在,求出m的取值范围;若不存在,请说明理由.
<0?若存在,求出m的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x﹣a,g(x)=a|x|,a∈R.
(1)设F(x)=f(x)﹣g(x). ①若a= ![]() ,求函数y=F(x)的零点;
,求函数y=F(x)的零点;
②若函数y=F(x)存在零点,求a的取值范围.
(2)设h(x)=f(x)+g(x),x∈[﹣2,2],若对任意x1 , x2∈[﹣2,2],|h(x1)﹣h(x2)|≤6恒成立,试求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】葫芦岛市某工厂党委为了研究手机对年轻职工工作和生活的影响情况做了一项调查:在厂内用简单随机抽样方法抽取了30名25岁至35岁的职工,对其“每十天累计看手机时间”(单位:小时)进行调查,得到茎叶图如下.所抽取的男职工“每十天累计看手机时间”的平均值和所抽取的女生 “每十天累计看手机时间”的中位数分别是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】葫芦岛市某高中进行一项调查:2012年至2016年本校学生人均年求学花销 ![]() (单位:万元)的数据如下表:
(单位:万元)的数据如下表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 |
年份代号 | 1 | 2 | 3 | 4 | 5 |
年求学花销 | 3.2 | 3.5 | 3.8 | 4.6 | 4.9 |
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
(1)求 ![]() 关于
关于 ![]() 的线性回归方程;
的线性回归方程;
(2)利用(1)中的回归方程,分析2012年至2016年本校学生人均年求学花销的变化情况,并预测该地区2017年本校学生人均年求学花销情况.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱柱ABCD﹣A1B1C1D1中,侧面A1ADD1⊥底面ABCD,D1A=D1D= ![]() ,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点. 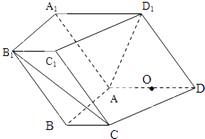
(1)求证:A1O∥平面AB1C;
(2)求锐二面角A﹣C1D1﹣C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,几何体ABCDE中,△ABC是正三角形,EA和DC都垂直于平面ABC,且EA=AB=2a,DC=a,F、G分别为EB和AB的中点. 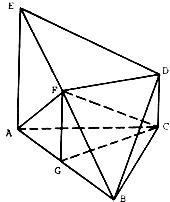
(1)求证:FD∥平面ABC;
(2)求二面角B﹣FC﹣G的正切值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com