
| A. | 命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0” | |
| B. | “x=1”是“x2-3x+2=0”的充分不必要条件 | |
| C. | 命题“在△ABC中,若A>B,则sinA>sinB”的逆命题为假命题 | |
| D. | 对于命题p:?x∈R,使得x2+x-1<0,则¬p:?x∈R,则x2+x+1≥0 |
分析 A.根据逆否命题的定义进行判断
B.根据充分条件和必要条件的定义进行判断
C.根据四种命题真假之间的关系进行判断
D.根据含有量词的命题的否定进行判断
解答 解:A.命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0”,正确,
B.由x2-3x+2=0得x=1或x=2,即“x=1”是“x2-3x+2=0”的充分不必要条件,正确
C.命题“在△ABC中,若A>B,则sinA>sinB”的逆命题为“在△ABC中,若sinA>sinB,则A>B,
若sinA>sinB,由正弦定理得a>b,即等价为A>B,即逆否命题为真命题,故C判断错误.
D.命题p:?x∈R,使得x2+x-1<0,则¬p:?x∈R,则x2+x+1≥0,正确,
故选:C
点评 本题主要考查命题的真假判断,涉及四种命题的真假关系,充分条件和必要条件的判断以及含有量词的命题的否定,综合性较强.


科目:高中数学 来源: 题型:解答题
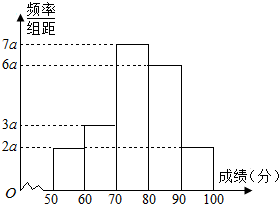 某班40名学生某次数学考试成绩(单位:分)的频率分布直方图如图所示.(学生成绩都在[50,100]之间)
某班40名学生某次数学考试成绩(单位:分)的频率分布直方图如图所示.(学生成绩都在[50,100]之间)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
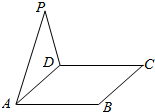 如图,△ADP为正三角形,四边形ABCD为正方形,平面PAD⊥平面ABCD.M为平面ABCD内的一动点,且满足MP=MC.则点M在正方形ABCD内的轨迹为(O为正方形ABCD的中心)( )
如图,△ADP为正三角形,四边形ABCD为正方形,平面PAD⊥平面ABCD.M为平面ABCD内的一动点,且满足MP=MC.则点M在正方形ABCD内的轨迹为(O为正方形ABCD的中心)( )| A. | 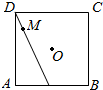 | B. | 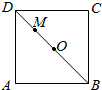 | C. |  | D. | 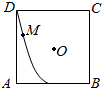 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
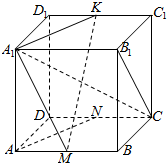 如图所示,M、N、K分别是正方体ABCD-A1B1C1D1的棱AB,CD,C1D1的中点.求证:
如图所示,M、N、K分别是正方体ABCD-A1B1C1D1的棱AB,CD,C1D1的中点.求证:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | -2 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com