
分析 (1)将$ρsin({θ-\frac{2π}{3}})=-\sqrt{3}$利用和差公式打开;根据x=ρcosθ,y=ρsinθ带入可得直线l和⊙C的普通方程.
(2)利用圆截直线的弦长公式求|AB|即可
解答 解:(1)直线l的方程为$ρsin({θ-\frac{2π}{3}})=-\sqrt{3}$,
可得:ρsinθcos$\frac{2π}{3}$-ρcosθsin$\frac{2π}{3}$=-$\sqrt{3}$
?-$\frac{1}{2}$y-$\frac{\sqrt{3}}{2}$x=$-\sqrt{3}$
即:$\sqrt{3}x+y=2\sqrt{3}$.
⊙C的极坐标方程为ρ=4cosθ+2sinθ.
可得:ρ2=4ρcosθ+2ρsinθ,
?x2+y2=4x+2y
即:x2+y2-4x-2y=0,
故得直线l的普通方程为:$\sqrt{3}x+y=2\sqrt{3}$;⊙C的普通方程为:x2+y2-4x-2y=0.
(2)由x2+y2-4x-2y=0,可知圆心为(2,1),半径r=$\sqrt{5}$,
那么:圆心到直线的距离d=$\frac{|2\sqrt{3}+1-2\sqrt{3}|}{2}=\frac{1}{2}$,
∴|AB|=2$\sqrt{{r}^{2}-{d}^{2}}=\sqrt{19}$
故得直线l与圆⊙C交于A,B两点间的弦AB长为$\sqrt{19}$.
点评 本题主要考查了极坐标方程与直角坐标方程的互换和圆心到直线的距离公式的运用.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:填空题
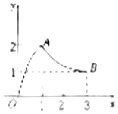 如图,函数f(x)的图象是曲线OAB,其中点O,A,B的坐标分别为(0,0),(1,2),(3,1),则$f[{\frac{1}{f(3)}}]$的值等于2.
如图,函数f(x)的图象是曲线OAB,其中点O,A,B的坐标分别为(0,0),(1,2),(3,1),则$f[{\frac{1}{f(3)}}]$的值等于2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
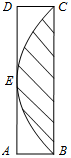 如图所示矩形ABCD边长AB=1,AD=4,抛物线顶点为边AD的中点E,且B,C两点在抛物线上,则从矩形内任取一点落在抛物线与边BC围成的封闭区域(包含边界上的点)内的概率是$\frac{2}{3}$.
如图所示矩形ABCD边长AB=1,AD=4,抛物线顶点为边AD的中点E,且B,C两点在抛物线上,则从矩形内任取一点落在抛物线与边BC围成的封闭区域(包含边界上的点)内的概率是$\frac{2}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com