Question

5．在如图所示的圆型图案中有12片树叶，构成树叶的圆弧均相同且所对的圆心角为$\frac{π}{3}$，若在圆内随机取一点，则此点取自树叶（即图中阴影部分）的概率是（　　）

• A． 2-$\frac{{3\sqrt{3}}}{π}$
• B． 4-$\frac{{6\sqrt{3}}}{π}$
• C． $\frac{1}{3}-\frac{{\sqrt{3}}}{2π}$
• D． $\frac{2}{3}$

Answer 1

分析 根据题意，12片树叶是由24个相同的弓形组成，计算弓形的面积，利用几何概率的计算公式求解即可．

解答 解：设圆的半径为r，如图所示，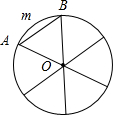

12片树叶是由24个相同的弓形组成，
且弓形AmB的面积为
S_弓形=$\frac{1}{6}$πr²-$\frac{1}{2}$•r²•sin$\frac{π}{3}$=$\frac{1}{6}$πr²-$\frac{\sqrt{3}}{4}$r²；
∴所求的概率为
P=$\frac{{24S}_{弓形}}{{S}_{圆}}$=$\frac{24×（\frac{1}{6}{πr}^{2}-{\frac{\sqrt{3}}{4}r}^{2}）}{{πr}^{2}}$=4-$\frac{6\sqrt{3}}{π}$．
故选：B．

点评 本题考查了几何概型的概率计算问题，是基础题．