
分析 根据题意,令sinx=$\frac{1}{3}$tanx,结合x∈[0,π]求出x的值,得出三个点A、B、C的坐标,即可计算△ABC的面积.
解答 解:根据题意,令sinx=$\frac{1}{3}$tanx,即sinx(1-$\frac{1}{3cosx}$)=0,解得sinx=0,或1-$\frac{1}{3cosx}$=0,
即sinx=0或cosx=$\frac{1}{3}$.
又x∈[0,π],∴x=0或x=π,或x=arccos$\frac{1}{3}$,∴点A(0,0),B(π,0),C(arccos$\frac{1}{3}$,$\frac{2\sqrt{2}}{3}$),
∴△ABC的面积为$\frac{1}{2}$•|AB|•|yC|=$\frac{1}{2}•π•\frac{2\sqrt{2}}{3}$=$\frac{\sqrt{2}}{3}$π,
故答案为:$\frac{{\sqrt{2}π}}{3}$.
点评 本题考查了三角函数的图象与性质的应用问题,属于中档题.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{1+k}$ | B. | $\frac{1}{k}$ | C. | $\frac{1}{{e({1+k})}}$ | D. | $\frac{e}{1+k}$ |
查看答案和解析>>
科目:高中数学 来源:2017届陕西汉中城固县高三10月调研数学(文)试卷(解析版) 题型:选择题
为了得到函数 ,
, 的图象,只需把函数
的图象,只需把函数 ,
, 的图象上所有点的( )
的图象上所有点的( )
A.横坐标伸长到原来的2倍,纵坐标不变
B.纵坐标伸长到原来的2倍,横坐标不变
C.横坐标缩短到原来的 倍,纵坐标不变
倍,纵坐标不变
D.纵坐标缩短到原来的 倍,横坐标不变
倍,横坐标不变
查看答案和解析>>
科目:高中数学 来源:2017届陕西汉中城固县高三10月调研数学(理)试卷(解析版) 题型:解答题
选修4—1:几何证明选讲
如图,△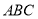 是圆
是圆 的内接三角形,
的内接三角形, 是
是 的延长线上一点,且
的延长线上一点,且 切圆
切圆 于点
于点 .
.

(1)求证: ;
;
(2)若 ,且
,且 ,求
,求 的长.
的长.
查看答案和解析>>
科目:高中数学 来源:2017届陕西汉中城固县高三10月调研数学(理)试卷(解析版) 题型:选择题
为了得到函数 ,
, 的图象,只需把函数
的图象,只需把函数 ,
, 的图象上所有点的( )
的图象上所有点的( )
A.横坐标伸长到原来的2倍,纵坐标不变
B.纵坐标伸长到原来的2倍,横坐标不变
C.横坐标缩短到原来的 倍,纵坐标不变
倍,纵坐标不变
D.纵坐标缩短到原来的 倍,横坐标不变
倍,横坐标不变
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com