
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 图象连续的函数f(x)在区间(a,b)上一定存在最值 | |
| B. | 函数的极小值可能大于极大值 | |
| C. | 函数的最小值一定是极小值 | |
| D. | 函数的极小值一定是最小值 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
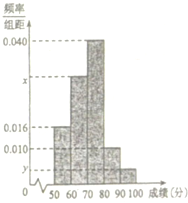 某中学举行了一次“环保知识竞赛”活动,为了了解本次竞赛学生成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本容量为n)进行统计,按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出如图所示的频率分布直方图,但由于不慎丢失了部分数据.已知得分在[50,60)的有8人,在[90,100)的有2人,由此推测频率分布直方图中的x=( )
某中学举行了一次“环保知识竞赛”活动,为了了解本次竞赛学生成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本容量为n)进行统计,按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出如图所示的频率分布直方图,但由于不慎丢失了部分数据.已知得分在[50,60)的有8人,在[90,100)的有2人,由此推测频率分布直方图中的x=( )| A. | 0.04 | B. | 0.03 | C. | 0.02 | D. | 0.01 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | S2>S3>S1 | B. | S1>S3>S2 | C. | S2>S1>S3 | D. | S1>S2>S3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
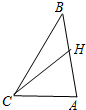 如图,在△ABC中,已知CA=2,CB=3,∠ACB=60°.
如图,在△ABC中,已知CA=2,CB=3,∠ACB=60°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com