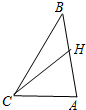Question

20．如图，在△ABC中，已知CA=2，CB=3，∠ACB=60°．
（1）求$\overrightarrow{CA}$•$\overrightarrow{CB}$
 （2）若H为AB的中点，试用向量知识求CH的长．

Answer 1

分析 （1）直接利用数量积公式求得$\overrightarrow{CA}$•$\overrightarrow{CB}$；
（2）由向量加法的三角形法则把$\overrightarrow{CH}$用$\overrightarrow{CA}、\overrightarrow{CB}$表示，结合向量模的平方等于向量的平方求得CH的长．

解答 解：（1）∵CA=2，CB=3，∠ACB=60°，
∴$\overrightarrow{CA}$•$\overrightarrow{CB}$=$|\overrightarrow{CA}||\overrightarrow{CB}|cos∠ACB=2×3×cos60°$=$2×3×\frac{1}{2}=3$；
（2）∵H为AB的中点，
∴$\overrightarrow{CH}=\frac{1}{2}（\overrightarrow{CA}+\overrightarrow{CB}）$，
则$|\overrightarrow{CH}|=\frac{1}{2}|\overrightarrow{CA}+\overrightarrow{CB}|=\frac{1}{2}\sqrt{（\overrightarrow{CA}+\overrightarrow{CB}）^{2}}$=$\frac{1}{2}\sqrt{{\overrightarrow{CA}}^{2}+{\overrightarrow{CB}}^{2}+2\overrightarrow{CA}•\overrightarrow{CB}}$=$\frac{1}{2}\sqrt{4+9+2×3}=\frac{1}{2}\sqrt{19}$．
∴CH的长为$\frac{\sqrt{19}}{2}$．

点评 本题考查平面向量的数量积运算，考查向量加法的平行四边形法则，是中档题．