
分析 (1)设等比数列{an}的公比为q,由题意可得q的方程,解方程验证递增可得;
(2)反证法:假设数列{an}中三项am,an,ap且m<n<p,由等差数列可得mnp的式子,推理产生奇数等于偶数的矛盾可得.
解答 (1)解:设等比数列{an}的公比为q,
由题意可得a1+a2+a3=$\frac{4}{q}+4+4q=14$,
解得q=$\frac{1}{2}$或q=2,又a2=4且{an}是递增的等比数列,
∴q=2,∴数列{an}的通项公式为${a_n}={2^n}$;
(2)证明:假设数列{an}中三项am,an,ap且m<n<p,
∴由等差数列可得2an=am+ap,
∴2n=2m-1+2p-1,∴2n-m+1=1+2p-m…(*),
∵m<n<p,∴p-m≥2,n-m≥1,
∴(*)式左边是偶数,右边是奇数,矛盾,
∴数列{an}中任意三项不能构成等差数列
点评 本题考查等差数列的通项公式,涉及反证法和解方程的思想,属中档题.


科目:高中数学 来源: 题型:选择题
| A. | 不全相等 | B. | 都相等,且为$\frac{8}{59}$ | C. | 均不相等 | D. | 都相等,且为$\frac{1}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
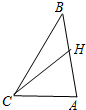 如图,在△ABC中,已知CA=2,CB=3,∠ACB=60°.
如图,在△ABC中,已知CA=2,CB=3,∠ACB=60°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-$\frac{1}{2}$) | B. | (-∞,-$\frac{1}{2}$] | C. | (-∞,-2] | D. | (-∞,-2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com