
分析 (1)由根与系数的关系写出sinα+cosα=$\frac{1}{5}$,sinα•cosα=$\frac{m}{5}$,利用同角三角函数的关系,即可求得m的值;
(2)根据同角的基本关系求得tanx的值,利用诱导公式化简,求得原式的值;
(3)根据立方和公式,即可求得sin3α+cos3α的值.
解答 解:(1)sinα和cosα是方程5x2-x+m=0的两实根.
sinα+cosα=$\frac{1}{5}$,sinα•cosα=$\frac{m}{5}$,
sin2α+cos2α=(sinα+cosα)2-2sinαcosα=1
$\frac{1}{25}$-$\frac{2m}{5}$=1
m=-$\frac{12}{5}$,
(2)sinα和cosα是方程25x2-5x-12=0的两实根.α∈(0,π)时,sinα>0,
∴sinα=$\frac{4}{5}$,cosα=-$\frac{3}{5}$,或sinα=-$\frac{3}{5}$,cosα=$\frac{4}{5}$(舍去),
∴tanα=-$\frac{4}{3}$,
∴$\frac{1}{tan(3π-α)}$=$-\frac{1}{tanα}$=$\frac{3}{4}$;
(3)sin3α+cos3α=(sinα+cosα)(sin2α+cos2α-sinαcosα),
=(sinα+cosα)(1-sinαcosα),
∵sinα=$\frac{4}{5}$,cosα=-$\frac{3}{5}$,或sinα=-$\frac{3}{5}$,cosα=$\frac{4}{5}$,
∴sin3α+cos3α=$\frac{1}{5}$×(1+$\frac{12}{25}$)=$\frac{37}{125}$.
点评 本题考查韦达定理与求三角求值相结合,诱导公式的应用,属于中档题.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:高中数学 来源: 题型:解答题
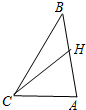 如图,在△ABC中,已知CA=2,CB=3,∠ACB=60°.
如图,在△ABC中,已知CA=2,CB=3,∠ACB=60°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-$\frac{1}{2}$) | B. | (-∞,-$\frac{1}{2}$] | C. | (-∞,-2] | D. | (-∞,-2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com