
| AΘ° | -$\frac{{\sqrt{21}}}{7}$ | BΘ° | $\frac{{\sqrt{21}}}{7}$ | CΘ° | $\frac{{\sqrt{21}}}{14}$ | DΘ° | -$\frac{3}{5}$ |
Ζ÷Έω ΗυΨί“―÷ΣΘ§«σ≥ωœρΝΩ$\overrightarrow{a}$Θ§$\overrightarrow{b}$ΒΡΡΘΘ§ΦΑ$\overrightarrow{a}$•$\overrightarrow{b}$Θ§¥ζ»κœρΝΩΦ–Ϋ«ΙΪ ΫΘ§Ω…ΒΟ¥πΑΗΘ°
Ϋβ¥π ΫβΘΚΓΏ$\overrightarrow{e}$1Θ§$\overrightarrow{e}$2 «Φ–Ϋ«ΈΣ120ΓψΒΡΝΫΗωΒΞΈΜœρΝΩΘ°
Γύ$\overrightarrow{e}$12=$\overrightarrow{e}$22=|$\overrightarrow{e}$1|2=|$\overrightarrow{e}$2|2=1Θ§
$\overrightarrow{e}$1•$\overrightarrow{e}$2=-$\frac{1}{2}$Θ§
Ι |$\overrightarrow{a}$|2=4$\overrightarrow{e}$12+$\overrightarrow{e}$22+4$\overrightarrow{e}$1•$\overrightarrow{e}$2=3Θ§Φ¥|$\overrightarrow{a}$|=$\sqrt{3}$Θ§
|$\overrightarrow{b}$|2=4$\overrightarrow{e}$12+$\overrightarrow{e}$22-4$\overrightarrow{e}$1•$\overrightarrow{e}$2=7Θ§Φ¥|$\overrightarrow{b}$|=$\sqrt{7}$Θ§
$\overrightarrow{a}$•$\overrightarrow{b}$=-4$\overrightarrow{e}$12+$\overrightarrow{e}$22=-3Θ§
Ι $\overrightarrow{a}$=2$\overrightarrow{e}$1+$\overrightarrow{e}$2ΚΆ$\overrightarrow{b}$=$\overrightarrow{e}$2-2$\overrightarrow{e}$1ΒΡΦ–Ϋ«Π»ΒΡ”ύœ“÷ΒΘ§
cosΠ»=$\frac{-3}{\sqrt{3}•\sqrt{7}}$=-$\frac{{\sqrt{21}}}{7}$Θ§
Ι ―ΓΘΚA
ΒψΤά ±ΨΧβΩΦ≤ιΒΡ÷Σ ΕΒψ «œρΝΩΒΡ ΐΝΩΜΐ‘ΥΥψΘ§œρΝΩΒΡΡΘΘ§œρΝΩΦ–Ϋ«ΙΪ ΫΘ§Ρ―Ε»÷–ΒΒΘ°


 ±Π±¥ΦΤΜ°ΤΎΡ©≥ε¥ΧΕα100Ζ÷œΒΝ–¥πΑΗ
±Π±¥ΦΤΜ°ΤΎΡ©≥ε¥ΧΕα100Ζ÷œΒΝ–¥πΑΗ ΡήΩΦ ‘»ΪΡή100Ζ÷œΒΝ–¥πΑΗ
ΡήΩΦ ‘»ΪΡή100Ζ÷œΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | 30÷÷ | BΘ° | 24÷÷ | CΘ° | 18÷÷ | DΘ° | 12÷÷ |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | 2x+Π–y-Π–=0 | BΘ° | 2x-Π–y-Π–=0 | CΘ° | $x-Π–y-\frac{Π–}{2}=0$ | DΘ° | $x+Π–y-\frac{Π–}{2}=0$ |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | 4 | BΘ° | 2 | CΘ° | 1 | DΘ° | $\frac{2}{3}$ |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
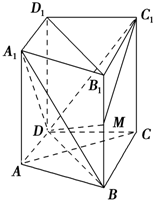 »γΆΦΥυ ΨΘ§‘Ύ÷±ΥΡάβ÷υABCD-A1B1C1D1÷–Θ§DB=BCΘ§DBΓΆACΘ§ΒψM «άβBB1…œ“ΜΒψΘ°
»γΆΦΥυ ΨΘ§‘Ύ÷±ΥΡάβ÷υABCD-A1B1C1D1÷–Θ§DB=BCΘ§DBΓΆACΘ§ΒψM «άβBB1…œ“ΜΒψΘ°≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | -1ΓήxΓή3 | BΘ° | xΓή-1 | CΘ° | xΓί3 | DΘ° | xΘΦ-1ΜρxΘΨ3 |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
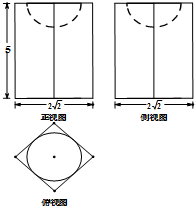
| AΘ° | 20-2Π– | BΘ° | 40-$\frac{2}{3}$Π– | CΘ° | 20-$\frac{2}{3}$Π– | DΘ° | 20-$\frac{4}{3}$Π– |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com