
(2005•辽宁)已知函数f(x)= (x≠﹣1).设数列{an}满足a1=1,an+1=f(an),数列{bn}满足bn=|an﹣
(x≠﹣1).设数列{an}满足a1=1,an+1=f(an),数列{bn}满足bn=|an﹣ |,Sn=b1+b2+…+bn(n∈N*).
|,Sn=b1+b2+…+bn(n∈N*).
(Ⅰ)用数学归纳法证明bn≤ ;
;
(Ⅱ)证明Sn< .
.
见解析
【解析】
试题分析:(Ⅰ)我们用数学归纳法进行证明,先证明不等式bn≤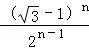 当n=1时成立,再假设不等式bn≤
当n=1时成立,再假设不等式bn≤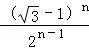 当n=k(k≥1)时成立,进而证明当n=k+1时,不等式bn≤
当n=k(k≥1)时成立,进而证明当n=k+1时,不等式bn≤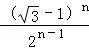 也成立,最后得到不等式bn≤
也成立,最后得到不等式bn≤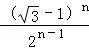 对于所有的正整数n成立;
对于所有的正整数n成立;
(Ⅱ)根据(Ⅰ)的结论,我们可以利用放缩法证明Sn<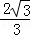 ,放缩后可以得到一个等比数列,然后根据等比数列前n项公式,即可得到答案.
,放缩后可以得到一个等比数列,然后根据等比数列前n项公式,即可得到答案.
证明:(Ⅰ)当x≥0时,f(x)=1+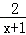 ≥1.
≥1.
因为a1=1,所以an≥1(n∈N*).
下面用数学归纳法证明不等式bn≤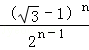 .
.
(1)当n=1时,b1= ﹣1,不等式成立,
﹣1,不等式成立,
(2)假设当n=k时,不等式成立,即bk≤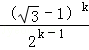 .
.
那么bk+1=|ak+1﹣ |=
|=
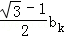 ≤
≤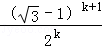 .
.
所以,当n=k+1时,不等式也成立.
根据(1)和(2),可知不等式对任意n∈N*都成立.
(Ⅱ)由(Ⅰ)知,bn≤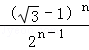 .
.
所以Sn=b1+b2+…+bn≤( ﹣1)+
﹣1)+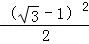 +…+
+…+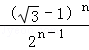 =(
=( ﹣1)•
﹣1)•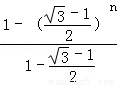 <(
<(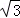 ﹣1)•
﹣1)•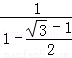 =
=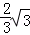 .
.
故对任意n∈N*,Sn<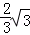 .
.


科目:高中数学 来源:[同步]2014年新人教A版选修4-6 2.4一次同余方程练习卷(解析版) 题型:填空题
设a、b、m(m>0)为整数,若a和b被m除得的余数相同,则称a和b对模m同余,记为a≡b(bmodm);已知a=1+C201+C202•2+C203•22+…+C2020•219,b≡a(bmod10),则满足条件的正整数b中,最小的两位数是 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-6 1.1整除练习卷(解析版) 题型:填空题
用“秦九韶算法”计算多项式f(x)=4x5﹣3x4+4x3﹣2x2﹣2x+3的值,当x=3时,求多项式值的过程中,要经过 次乘法运算和 次加法运算.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-6 1.1整除练习卷(解析版) 题型:选择题
今天是星期四,再过22009天后的那一天是( )
A.星期一 B.星期二 C.星期五 D.星期六
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-6 1.1整除练习卷(解析版) 题型:选择题
(2011•江西模拟)在算式“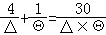 ”中,△、Θ都为正整数,且它们的倒数之和最小,则△、Θ的值分别为( )
”中,△、Θ都为正整数,且它们的倒数之和最小,则△、Θ的值分别为( )
A.6,6 B.10,5 C.14,4 D.18,3
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-5 4.1数学归纳法练习卷(解析版) 题型:选择题
用数学归纳法证明“2n>n2+1对于n≥n0的自然数n都成立”时,第一步证明中的起始值n0应取( )
A.2 B.3 C.5 D.6
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-5 3.3排序不等式练习卷(解析版) 题型:解答题
若a1≤a2≤…≤an,而b1≥b2≥…≥bn或a1≥a2≥…≥an而b1≤b2≤…≤bn,证明: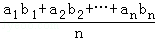 ≤(
≤(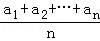 )•(
)•(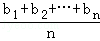 ).当且仅当a1=a2=…=an或b1=b2=…=bn时等号成立.
).当且仅当a1=a2=…=an或b1=b2=…=bn时等号成立.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-5 2.3反证法与放缩法练习卷(解析版) 题型:选择题
用反证法证明命题:“一个三角形中不能有两个直角”的过程归纳为以下三个步骤:
①A+B+C=90°+90°+C>180°,这与三角形内角和为180°相矛盾,A=B=90°不成立;
②所以一个三角形中不能有两个直角;
③假设三角形的三个内角A、B、C中有两个直角,不妨设A=B=90°,
正确顺序的序号为( )
A.①②③ B.①③② C.②③① D.③①②
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com